Tak, cień może przekroczyć prędkość światła.

Można się o tym przekonać analizując prosty układ złożony ze źródła światła, ruchomej przysłony i ekranu następującej postaci. Źródłem światła jest świetlówka $s$ w kształcie odcinka prostej. Przysłona $p$ ma kształt połówki powierzchni bocznej walca o promieniu $r$ otrzymanej poprzez przecięcie tej powierzchni płaszczyzną przechodzącą przez jej oś. Wreszcie ekran $e$ ma kształt powierzchni bocznej walca o promieniu $R>r$. Świetlówka umieszczona jest na osi ekranu, a oś przysłony (tzn. oś powierzchni bocznej walca, z której ta przysłona powstała) pokrywa się z osią ekranu. Przysłonę wprawiono w ruch obrotowy wokół świetlówki ze stałą prędkością kątową $\omega$, przez co świetlówka razem z przysłoną podobne są do tzw. „koguta” montowanego na dachach pojazdów uprzywilejowanych. Przyjmijmy ponadto dla uproszczenia, że fotony emitowane przez świetlówkę rozchodzą się wzdłuż prostych prostopadłych do świetlówki. Przekrój poprzeczny przez tak skonstruowany układ przedstawiony jest na poniższym rysunku.

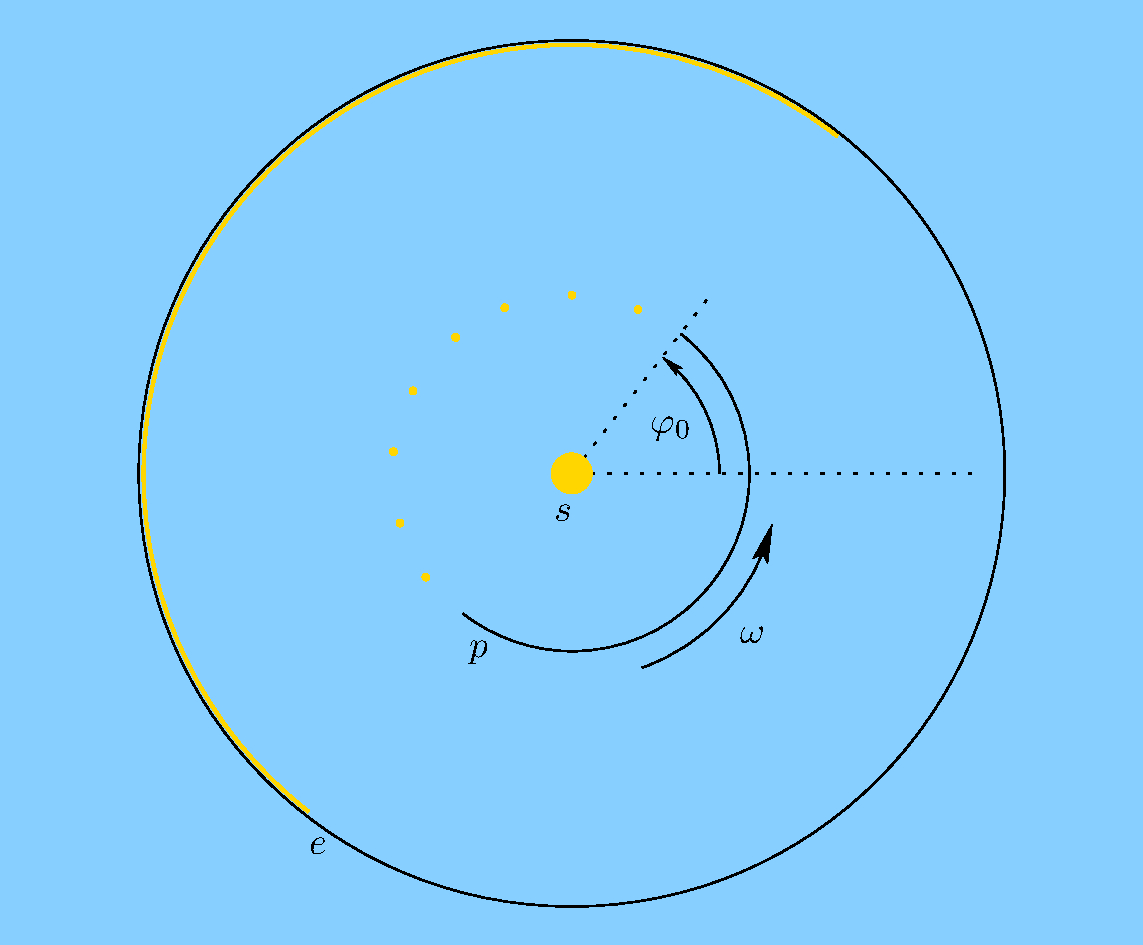
Rozważmy teraz fotony, które w chwili $t_0$ znajdują się w odległości $r$ od świetlówki. Część z nich w tym momencie zostanie pochłonięta przez przysłonę, a część będzie kontynuowała ruch w kierunku ekranu. Jeśli wprowadzimy współrzędną kątową $\varphi$ mierzoną od wykropkowanej na rysunku „poziomej” półprostej i przyjmiemy, że w chwili $t_0$ położenie przedniej krawędzi przysłony jest dane przez wartość $\varphi_0$ tej współrzędnej, to współrzędna kątowa fotonów, które nie zostaną pochłonięte w chwili $t_0$ przez przysłonę, będzie zmieniała się od $\varphi_0$ do $\varphi_0+\pi$ — na rysunku 1 niektóre z tych fotonów przedstawione są symbolicznie za pomocą żółtych kropek.

Na dotarcie do ekranu każdy z rozważanych fotonów potrzebuje czasu

$$\Delta t=\frac{R-r}{c},$$
gdzie $c$ jest wartością prędkości światła. Zatem w chwili
$$\begin{equation} t_1=t_0+\Delta t=t_0+\frac{R-r}{c} \label{t1} \end{equation}$$
oświetlona będzie ta część ekranu, w obszarze której współrzędna kątowa zmienia się od $\varphi_0$ do $\varphi_0+\pi$ — na rysunku 1 ta część zaznaczona jest za pomocą żółtego półkola. W konsekwencji w chwili $t_1$ cień będzie zajmował pozostałą część ekranu czyli część, w obszarze której współrzędna kątowa przyjmuje wartości z przedziału $$\begin{equation} [\,\varphi_0-\pi,\varphi_0\,]. \label{prze} \end{equation}$$
Bez straty ogólności możemy przyjąć, że funkcja
$$t\mapsto \omega t$$
opisuje zależność od czasu $t$ współrzędnej $\varphi$ przedniej krawędzi przysłony i tym samym ruch obrotowy całej przysłony. Zatem
$$\varphi_0=\omega t_0=\omega t_1-\omega \frac{R-r}{c},$$
gdzie w ostatnim kroku skorzystaliśmy z równania $\eqref{t1}$. Opierając się na powyższym wzorze i na postaci przedziału $\eqref{prze}$ wnioskujemy, że w chwili $t_1$ cień będzie obejmował tą część ekranu, w obszarze której współrzędna kątowa przyjmuje wartości z przedziału
$$\Big[\,\omega t_1-\omega \frac{R-r}{c}-\pi,\omega t_1-\omega \frac{R-r}{c}\,\Big]$$
— najmniejsza z powyższych wartości opisuje położenie tylnej krawędzi cienia, a największa jego przedniej krawędzi.

Ale $t_1$ jest dowolnie wybraną chwilą. W konsekwencji zależność współrzędnej $\varphi$ przedniej krawędzi cienia od czasu $t$ jest postaci

$$\varphi(t)= \omega t -\omega \frac{R-r}{c}.$$
Płynie stąd wniosek, że prędkość kątowa tej krawędzi cienia wynosi $\omega$, a ponieważ cień porusza się po powierzchni bocznej walca o promieniu $R$, więc wartość $v$ prędkości liniowej rozważanej krawędzi cienia jest dana wzorem
$$v=\omega R.$$

Widać stąd, że dla każdej niezerowej prędkości kątowej $\omega$ można tak dobrać promień $R$, aby wartość $v$ prędkości krawędzi cienia przewyższała wartość $c$ prędkości światła.