W skrócie: opisane zjawisko polega na tym, że przedmiot wyróżnia dwie polaryzacje światła, które przepuszcza z różnym opóźnieniem, a w konsekwencji w różnej fazie; przy innej polaryzacji światła padającego dzieli się ono na te dwie polaryzacje i łączy przy wyjściu z przedmiotu – i z powodu różnicy fazy na ogół uzyskuje wtedy inną polaryzację, niż początkowa, więc przechodzi przez polaryzator ustawiony prostopadle do początkowej polaryzacji (trzeba tu pamiętać, że światło o polaryzacji innej, niż przepuszczana przez polaryzator, albo prostopadła do niej, w polaryzatorze rozkłada się na dwie prostopadłe do siebie polaryzacje, i jedna jest przepuszczana, a druga pochłaniana, albo odchylana – więc z każdej polaryzacji, poza jedną, coś przechodzi – z natężeniem proporcjonalnym do kwadratu kosinusa kąta między polaryzacją światła, a ustawieniem polaryzatora; oraz że istnieją nie tylko polaryzacje liniowe – najczęściej pojawia się eliptyczna).

To zjawisko zmienia polaryzację światła, ale nie wydziela określonej polaryzacji – jeśli na przedmiot pada światło niespolaryzowane, to i wychodzi niespolaryzowane (jeśli nie liczyć zależności współczynnika odbicia od polaryzacji) – może łączyć się z różnicą współczynników załamania między dwiema polaryzacjami, ale na ogół jest ona dużo za mała, by można było ją wykorzystać do zbudowania polaryzatora. Można zbudować polaryzator wykorzystując odbicie pod kątem Brewstera, ale w tym opisane zjawisko będzie przeszkadzać – powód przedstawię na zdjęciach. I można wykorzystać to zjawisko w układzie interferencyjnym (o tym dalej, po opisie, co w takim materiale się dzieje, i rysunku) – ale to jest skomplikowane i technicznie bardzo trudne do wykonania.

W układzie ze skrzyżowanymi polaryzatorami wyraźnie widać nawet niewielkie zaburzenia polaryzacji przy przechodzeniu światła przez ośrodek, ponieważ drugi polaryzator usuwa to, co nie zostało zaburzone; natomiast do zbudowania polaryzatora zwykle potrzebna jest duża różnica przechodzenia światła w zależności od polaryzacji.

Wiele przeźroczystych materiałów ma anizotropię przenikalności dielektrycznej, a przez to współczynnika załamania światła. W polimerach taka anizotropia może zostać wytworzona np. poprzez deformację materiału (np. jego rozciągnięcie), której skutkiem jest pewne uporządkowanie cząstek polimeru (przewaga ułożenia bardziej wzdłuż kierunku rozciągnięcia, niż w poprzek).

W ośrodku izotropowym światło rozchodzi się niezależnie od kierunku, i długość jego fali nie zależy ani od kierunku, ani od polaryzacji – jest odwrotnie proporcjonalna do pierwiastka z przenikalności dielektrycznej ośrodka. W anizotropowym – długość fali zależy od kierunku jej pola elektrycznego, czyli od polaryzacji światła, i opis przechodzenia światła przez taki ośrodek staje się bardziej złożony.

Przenikalność dielektryczna jest związana z odwracalnym przesunięciem ładunków pod wpływem pola elektrycznego; w ośrodku izotropowym przesuwają się one w kierunku pola, i wielkość tego przesunięcia zależy tylko od wielkości pola, nie od kierunku; natomiast w anizotropowym na ogół w nieco innym – przez co fala powoduje dodatkowo drgania ładunków w kierunku prostopadłym do jej pola, a ona z kolei wytworzenie fali o innym kierunku pola. To komplikuje opis przechodzenia fali przez taki ośrodek – ale są kierunki wyróżnione, dla których ładunki przesuwają się w kierunku pola, i jeśli mamy falę o kierunku pola innym, niż któryś wyróżniony, to można jej pole rozłożyć na dwie składowe w wyróżnionych kierunkach i opisać falę jako sumę dwóch odrębnych fal, które nieco różnie się zachowują, ale już nie występuje oddziaływanie zmieniające jedną w drugą (podobne zjawisko występuje dla układu dwóch wahadeł *).

Te dwie fale przede wszystkim zwykle mają różne długości (zdarza się też, że biegną w różnych kierunkach, że nawet po wejściu światła do ośrodka prostopadle do jego powierzchni mamy w ośrodku jeden promień biegnący dalej w tym samym kierunku, i drugi, który biegnie w innym – żeby to było zauważalne, różnica współczynników załamania musi być spora – ale tutaj opisujemy tylko wpływ różnicy długości fali **), przez co powstaje różnica fazy między tymi falami.

Jeśli fala wchodząca do ośrodka miała jakąś określoną polaryzację, to przełoży się ona na stosunek amplitud tych dwu fal w ośrodku, oraz fazę zgodną, albo przeciwną; gdyby po przejściu przez ośrodek różnica faz pozostała niezmieniona (bo różnica ilości długości fali w ośrodku dla obu fal byłaby liczbą całkowitą), to złożyłyby się one na falę wychodzącą identyczną z tą, która weszła do ośrodka.

Wygodnie będzie używać pojęcia drogi optycznej, równej całce współczynnika załamania (i jednocześnie skrócenia fali) po drodze światła. Jeśli różnica dróg optycznych dla obu fal jest wielokrotnością długości fali w próżni, to ich różnica fazy nie ulega zmianie.

Jeśli jednak występuje różnica dróg optycznych o pół długości fali (płytkę z przeźroczystego materiału dającą taką różnicę dróg optycznych nazywa się półfalówką), to różnica faz zmieni się na przeciwną, i złożą się one na falę o polaryzacji, która względem polaryzacji wchodzącej fali będzie jej lustrzanym odbiciem w płaszczyźnie polaryzacji dowolnej z fal składowych w ośrodku – w szczególności, przy kącie 45° między kierunkiem polaryzacji fali wchodzącej i wyróżnionym kierunkiem w materiale płytki polaryzacja wychodzącej fali będzie prostopadła do polaryzacji fali wchodzącej.

Przy różnicy o ćwierć długości fali (taką płytkę nazywa się ćwierćfalówką) i polaryzacji fali wchodzącej pod kątem 45° do fal składowych w ośrodku złożą się one na falę o polaryzacji kołowej – w ten sposób konstruuje się polaryzatory kołowe, składając polaryzator liniowy i płytkę z różnicą dróg optycznych o ćwierć długości fali, z kątem 45° między ich polaryzacjami. Zależnie od tego, w którą stronę będzie ten kąt, uzyskuje się polaryzację prawo-, albo lewoskrętną.

Inne różnice dróg optycznych, albo inne kąty, niż 0° i 90° będą dawać falę wychodzącą o polaryzacji eliptycznej.

Jeśli płytkę z przezroczystego dielektryka umieści się pomiędzy skrzyżowanymi polaryzatorami liniowymi, to wynik będzie zależny od kąta między płaszczyznami polaryzacji światła polaryzatorów i składowych fali w tej płytce (można wybrać dowolny z polaryzatorów i dowolną składową fali w płytce, i określać kąt pomiędzy nimi): jeśli ten kąt będzie 0°, albo 90°, to w płytce pojawi się tylko jedna fala, i wyjdzie z niej taka sama fala, jak wejdzie, więc drugi polaryzator ją pochłonie; największy wpływ płytki na przechodzenie światła będzie przy kącie 45° i przy różnicy dróg optycznych o pół długości fali.

Warto tu zauważyć, że przy długości fali 0,5 mikrona i grubości płytki 0,5 mm taką różnicę dróg optycznych uzyska się przy różnicy współczynników załamania o 0,0005 – a więc tysiąc razy mniejszej, niż różnica współczynnika załamania między szkłem i próżnią.

Zachowanie się fali dla różnicy dróg optycznych o pół długości fali i kąta 60° między wyróżnionym kierunkiem ośrodka, a polaryzacją fali, przedstawiłem na rysunku. Fioletowa linia to fala wchodząca, o długości 1; od z=1.25 zaczyna się, a dla z=2.5 kończy ośrodek, w którym dla polaryzacji pionowej (Y) fala jest 2x krótsza, a dla poziomej (X) 1.6x krótsza – w ośrodku mieszczą się 2 długości fali poziomej, i 2.5 długości fali pionowej – taka duża różnica współczynników załamania jest po to, by rysunek nie musiał zawierać setek długości fali; ten mniejszy obrazek zawiera animację:

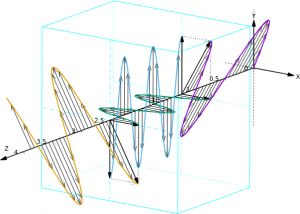
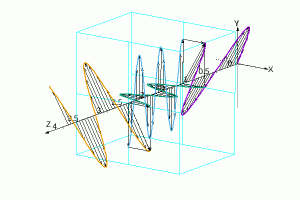
Fala wchodząca dzieli się na dwie fale w ośrodku, które przy wychodzeniu z niego na nowo się łączą, ale teraz faza pionowej się odwróciła, i polaryzacja fali po przejściu przez ośrodek zmieniła się na inną.

Warto tu zauważyć, że ta zmiana polaryzacji nie wpływa na natężenie światła przechodzącego przez płytkę, niezależnie od polaryzacji, jaką miało światło wchodzące, ani na równomierność rozkładu polaryzacji światła, jeśli było niespolaryzowane – każdej polaryzacji światła wchodzącego odpowiada jakaś polaryzacja światła wychodzącego, płytka wprowadza tylko ich zamiany (pomijam tu niewielką różnicę współczynników odbicia światła spowodowaną przez różnicę współczynników załamania).

Teoretycznie, mając półfalówkę (różnica nawet nie musi być równo o pół fali), można zbudować układ polaryzujący z pomocą interferencji: coś w stylu interferometru Macha-Zehndera – rozdzielić wiązkę światła na płytce półprzepuszczalnej, i skierować obie wiązki na drugą taką płytkę, wstawiając w jeden z torów płytkę dającą różnicę dróg optycznych między polaryzacjami o pół długości fali, a w drugi płytkę z materiału izotropowego – kiedy wiązki się spotkają, światło o jednej polaryzacji może być w przeciwnych fazach, o drugiej w zgodnych – w rezultacie uzyska się wiązkę spolaryzowaną liniowo. Ale po pierwsze, wymagałoby to dużej precyzji – błąd o kilkanaście nm (nanometrów – milionowych części mm) już wyraźnie pogorszy działanie polaryzatora, a 1/4 długości fali zniweczy je całkowicie – a po drugie, wynik prawdopodobnie byłby zależny od długości fali (to jeszcze by zależało od użytych materiałów), i od nawet niewielkich zmian temperatury.

Przy użyciu płytki ćwierćfalowej uzyskuje się polaryzację eliptyczną (płytka jest od Z=1,375 do Z=2,0, współczynniki załamania i polaryzacja światła wchodzącego takie same, jak poprzednio; uzyskanie polaryzacji kołowej wymagałoby kąta polaryzacji 45°):

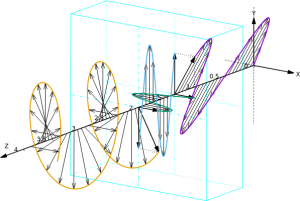
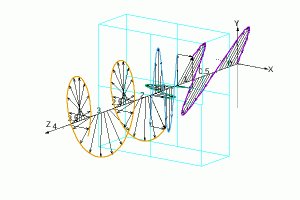
*) Chodzi tu o dwa identyczne wahadła nieco sprzężone ze sobą: po puszczeniu w ruch jednego z nich pojawia się i stopniowo narasta ruch drugiego, aż pierwsze przestaje się wahać, i waha się tylko drugie; potem znów pojawia się i narasta ruch pierwszego… energia przepływa między nimi raz w jedną, raz w drugą stronę. Można to opisać inaczej: wahadła mogą się wahać zgodnie, albo przeciwnie (i taki ruch nie będzie ulegał zmianie, poza zanikiem w wyniku strat energii), i okresy tych wahań są nieco różne; inne sposoby wahań są złożeniem tych dwóch – w szczególności wahanie się jednego zawiera tyle samo wahania zgodnego i przeciwnego, ze zgodną fazą dla pierwszego, a przeciwną dla drugiego; po pewnym czasie różnica faz przesunie się o pół okresu, i wtedy dla pierwszego wahadła fazy będą przeciwne, dla drugiego zgodne – czyli będzie wahać się tylko drugie. Fizycy mówią o modach wahań w takim układzie, i wyróżniają wśród nich mody własne, które nie zmieniają kształtu w czasie; są z nimi powiązane częstotliwości własne tego układu wahadeł. Podobną sytuację mamy dla anizotropowej płytki: dwie prostopadłe polaryzacje stanowią jej mody własne, one przechodzą bez zmian, a zmiany innych wynikają z różnicy długości fali pomiędzy tymi modami własnymi; nie zmienia się to, jak wchodzące światło podzieli się między te mody własne, ale zmienia się różnica fazy – dla wahadeł z powodu różnicy okresów wahań, dla światła z powodu różnicy długości fali.

**) W niniejszym opisie jest jeden wyróżniony kierunek, dla którego przenikalność jest inna, i jest on równoległy do powierzchni, na którą światło pada prostopadle; gdyby był on prostopadły, to dla pola równoległego do tej powierzchni przenikalność nie zależałaby od kierunku, natomiast gdyby był pod jakimś kątem pośrednim, to kierunek ruchu fali zależałby od polaryzacji.

Tę zależność kierunku od polaryzacji wykorzystuje się w polaryzatorach takich, jak pryzmat Nicola, ale wymaga to sporej różnicy kierunku między obiema polaryzacjami – od tego zależy zakres kątów, w jakim musi być światło, by taki polaryzator rozróżniał jego polaryzację.

Okulary polaryzujące światło są robione w inny sposób: jest w nich barwnik, którego cząsteczki pochłaniają światło o określonej polaryzacji, i przy wytwarzaniu szybki okularów ich ułożenie zostało uporządkowane poprzez rozciąganie materiału w jednym kierunku – cząsteczki barwnika ułożyły się wzdłuż tego kierunku. O ile dobrze się zorientowałem, jakaś folia użyta jako opakowanie do cukierków miała podobną właściwość, ale użyty w niej barwnik pochłaniał tylko pewien zakres światła widzialnego, i tylko ten zakres był polaryzowany.

Powyższy opis zakłada, że fala ma określoną długość – czyli światło jest monochromatyczne – a co będzie, jeśli jest światło białe, będące mieszaniną fal o różnych długościach?

Różnica dróg optycznych wyrażona w długości fali tego światła raczej nie będzie taka sama dla każdej barwy – a to oznacza, że dla różnych długości fali wynik oddziaływania płytki na spolaryzowane światło będzie różny – światło, które przejdzie, będzie kolorowe. Sama różnica dróg optycznych wyrażona np. w mikronach prawdopodobnie niewiele będzie zależeć od długości fali światła; wyrażona w długości fali światła będzie zmieniać się dużo bardziej – trzeba pamiętać, że zakres długości fali widziany przez oko to od około 0,4 µm do 0,8 µm – ta sama różnica drogi dla najkrótszych fal wprowadza 2 razy większe przesunięcie fazy, niż dla najdłuższych.

To, czy kolory będą widoczne, jest zależne od tej różnicy dróg optycznych: jeśli będzie ona duża, to układ będzie miał wiele wąskich pasm przepuszczania i pochłaniania światła – a oko może rozróżniać tylko trzy barwy, i zobaczy światło wychodzące jako białe. Powstawanie barw podlega tym samym regułom, co dla barw baniek mydlanych (zjawisko ich powstawania nazwano iryzacją – od Iris – imienia greckiej bogini tęczy – jakkolwiek mechanizm powstawania barw tęczy jest inny), albo dla barw pierścieni Newtona: we wszystkich tych sytuacjach mamy do czynienie z interferencją światła, które przechodzi po dwóch drogach i dochodzi w przeciwnej fazie, ale z niewielką różnicą drogi – ta różnica powoduje, że coś z tego światła zostaje.

Sprawdziłem, co widać, gdy umieści się polistyrenową łyżeczkę pomiędzy polaryzatorami – zdecydowanie widać kolory i to wskazuje na różnicę dróg optycznych rzędu mikrona, może nawet mniejszą. A to odpowiada różnicy współczynników załamania rzędu jednej tysięcznej (kryształy szpatu islandzkiego, z których wykonywano polaryzatory, mają różnicę około 0,17 – dużo większą).
<- Tak wyglądał układ do obserwacji.

Jako polaryzatory posłużyły okulary – te dalsze są 3D do TV (od zewnątrz polaryzacja kołowa, od wewnątrz pozioma), bliższe takie do redukcji odblasków (polaryzacja pionowa).

Dla elementu „szkatułki” od płyty DVD widać gęstość kolorowych plam wzrastającą w pobliżu pewnego punktu – to skutek szybkich zmian (w funkcji położenia) różnicy współczynników załamania światła o różnych polaryzacjach – prawdopodobnie pozostały tam duże naprężenia (tak się składa, że w w tym punkcie jest wypukłość, która wygląda na pozostałość po otworze w formie, w której był on odlewany).

Polaryzację można też uzyskać przez odbicie pod kątem Brewstera – fala odbita jest całkowicie spolaryzowana. Jeśli światło pada na przeźroczystą płytkę pod tym kątem, to część jego odbija się na zewnątrz od pierwszej powierzchni, reszta przechodzi przez płytkę, i część jej odbija się do wewnątrz płytki, przechodzi przez nią powtórnie i częściowo wychodzi. Ustawiając odpowiednio polaryzator można usunąć z odbitego światła co, co może się odbić pod kątem Brewstera, ale światło odbite wewnątrz może zmienić polaryzację, jeśli płytka ma anizotropię współczynnika załamania – przez polaryzator przejdzie to, co jest zniekształceniem polaryzacji światła spowodowanym przez tę anizotropię. Na zdjęciach obraz przedmiotu oglądanego poprzez polaryzator, ale bez polaryzacji światła, którym był oświetlony – zamiast tego było polaryzowanie poprzez odbicie pod kątem Brewstera. Wynik zależy od dokładności ustawienia i ograniczenia światła rozproszonego:

Można też w drugą stronę – tu wykorzystałem fakt, że światło monitora LCD jest spolaryzowane, więc jeśli odbija się pod kątem Brewstera w przeźroczystej płytce ustawionej w odpowiednim kierunku – takim, żeby jego polaryzacja nie pozwalała mu odbić się od powierzchni tej płytki – to zaburzenie polaryzacji przez anizotropię materiału płytki spowoduje pojawienie się kolorowego odbicia światła, które przeszło przez płytkę i odbiło się po drugiej jej stronie, mając już inną polaryzację – i widać to bez okularów polaryzujących. Ale wygląda to dużo gorzej – w otoczeniu było trochę światła niespolaryzowanego, które popsuło efekt (na drugim zdjęciu szkatułka płyty DVD, widoczne odbicie tekstu z ekranu monitora):

… i właśnie z tego powodu te przedmioty nie zachowują się jak polaryzatory światła odbitego pod kątem Brewstera.

Sprawdziłem jeszcze folię z opakowania filiżanek „Jan Niezbędny” – okazało się, że też wpływa na polaryzację światła, i to dość równomiernie. Umieszczona pomiędzy ekranem LCD, a okularami przepuszczającymi polaryzację prostopadłą do emitowanej przez ekran spowodowała przechodzenie światła w kolorze pomarańczowym; złożona podwójnie – w żółtym, potrójnie – w żółto-zielonym, poczwórnie – w niebiesko-zielonym. Oglądana poprzez okulary z polaryzacją kołową dla jednego kierunku była żółta, wyraźnie jaśniejsza od ekranu, dla drugiego niebieska, znacznie ciemniejsza – najwyraźniej światło żółte zmieniło polaryzację na kołową (a raczej czerwone i zielone były w takim samym stopniu podobne do tej, którą przepuszał jeden filtr okularów – bo monitor daje światło czerwone, zielone i niebieskie; niebieskie uzyskało polaryzację kołową w przeciwną stronę). Wygląda na to, że różnica dróg optycznych dla prostopadłych polaryzacji liniowych była 1/4, albo raczej 3/4 długości fali światła żółtego (i pewnie całą długość fali fioletowego, 1/2 czerwonego – to by pasowało do zaobserwowanych kolorów). Na pierwszym i trzecim zdjęciu na części powierzchni folia jest pojedynczo, na części podwójnie; na drugim na dużej części nawet poczwórnie (na małych fragmentach potrójnie); na czwartym potrójnie na środkowym pasku, a przy brzegach podwójnie; trzecie i czwarte używały polaryzatorów kołowych, o przeciwnym ustawieniu:

Więcej obrazków i zdjęć zamierzam zamieścić pod adresem: https://www.fuw.edu.pl/~jt/polaryzacja

Pozostawiłem poniżej odpowiedź, którą wpisał kolega, i mam do niej dwie uwagi:
(1) Przy różnicy dróg optycznych o pół długości fali interferencja, z którą tu mamy do czynienia, daje największą jasność, ale to nie znaczy, że musi być dokładne trafienie i przy innej różnicy nie będzie nic – przy różnicy o ćwierć długości fali będzie połowa tej jasności, i nie jest łatwo zauważyć, że przedmiot umieszczony pomiędzy polaryzatorami nie powoduje przechodzenia całego światła przez drugi polaryzator – jest takie złudzenie optyczne, że to, co jest na ciemnym tle, wygląda na jaśniejsze (pisał o tym Mickiewicz „Świeciły się z daleka pobielane ściany / Tym bielsze, że odbite od ciemnej zieleni”).
(2) Nie wpadłem na pomysł (a odpowiedź kolegi mi go podsunęła), że różnica współczynników załamania może być tylko przy powierzchni, a jest mechanizm, który może to powodować: jeśli polimeryzujący materiał płynie, końce tworzących się łańcuchów przyczepiają się do ścianek formy i z tego powodu układają się w kierunku przepływu.

Opisane właściwości ma płytka półfalowa. To nie jest polaryzator, jakkolwiek ma wpływ na polaryzację światła: światło o polaryzacji liniowej w jednej, wyróżnionej płaszczyźnie (płaszczyzna jest wyznaczona przez promień światła i kierunek polaryzacji, dlatego piszę o płaszczyźnie polaryzacji) wyprzedza o pół długości fali światło o prostopadłej polaryzacji.

Konsekwencją tego wyprzedzenia o pół długości fali jest zmiana kierunku polaryzacji dla światła spolaryzowanego liniowo w dowolnym kierunku innym, niż ten „szybki” i prostopadły do niego „wolny”: jeśli kierunek wektora elektrycznego opiszemy tak, że jego składowe w kierunku „szybkim” i „wolnym” miały zgodny znak, to opóźnienie spowoduje, że po przejściu przez płytkę ich znaki będą przeciwne – tak, jakby wektor odbił się w lustrze położonym w wyróżnionej płaszczyźnie. To właśnie powoduje zaobserwowany efekt – zmiana kierunku polaryzacji jest 2 razy większa od kąta obrotu płytki wokół promienia światła, podobnie jak przy obracaniu lusterkiem obraz w nim obraca się 2 razy szybciej.

Same właściwości płytki półfalowej są opisane w Wikipedii (i jest tam rysunek pokazujący przejście światła przez taką płytkę): przepuszcza całe światło nie polaryzując go, dla światła spolaryzowanego liniowo „odbija” kierunek polaryzacji, dla światła spolaryzowanego kołowo odwraca kierunek polaryzacji. Dwukrotnie cieńsza płytka ćwierćfalowa ma właściwość zamiany polaryzacji kołowej na liniową (i dla dwóch kierunków polaryzacji liniowej zamiany jej na kołową – to są kierunki pod kątem 45 stopni do wyróżnionej płaszczyzny) – takie płytki wykorzystuje się do konstruowania polaryzatorów kołowych (skleja się płytkę z polaryzatorem liniowym, pilnując tego kąta 45 stopni).

Wikipedia podaje, że takie płytki zwykle robi się z kwarcu (który ma współczynnik załamania nieco inny dla różnych kierunków polaryzacji), ale jest wiele innych substancji dwójłomnych, które także się do tego nadają, tylko trzeba odpowiednio dobrać kierunek wycięcia i grubość płytki. Pożądana jest raczej niewielka różnica współczynników załamania: dla kwarcu wychodzi grubość płytki 33µm (o ile się nie pomyliłem) i wycięcie tak cienkiej płytki już nie jest łatwe, lepiej chyba użyć fluorku magnezu, wtedy wyjdzie 50µm.

Dwójłomność wymaga anizotropii materiału. Występuje ona w kryształach, i to nie wszystkich – zależy od ich struktury, współczynniki załamania dla różnych kierunków wektora elektrycznego są na ogół różne, jeśli kryształ ma odpowiednią symetrię rozmieszczenia atomów – nie powinny być dwójłomne substancje, w których elementarna komórka kryształu jest sześcianem, bo wtedy z symetrii kryształu wynika równość współczynników załamania – żaden kierunek nie jest wyróżniony pod względem współczynnika załamania. Jeśli jednak elementarna komórka kryształu jest np. prostopadłościanem o różnych długościach krawędzi, albo graniastosłupem o podstawie sześciokątnej, to kryształ ma dużą szansę był dwójłomny.

Dotyczy to jednak monokryształu, bądź niewielu złączonych ze sobą kryształów – jeśli jest ich wiele (substancja jest polikrystaliczna), i są ustawione przypadkowo, to średni współczynnik załamania jest taki sam dla różnych kierunków polaryzacji i dwójłomności nie widać. Jest też wiele substancji stałych, w których atomy nie tworzą uporządkowanej sieci (do takich należy np. szkło i tworzywa sztuczne) – w zasadzie nie powinny one być dwójłomne, jeśli w każdym kierunku ich struktura jest taka sama. Może jednak nie być taka sama, jeśli np. w substancji są naprężenia (mogą być wewnętrzne, powstałe podczas produkcji), bądź zostało w nich „zamrożone” pole elektryczne, które oddziaływało na substancję podczas jej krzepnięcia, a nawet jest możliwe, że łańcuchy atomów (a w tworzywach sztucznych są one długie) zostały uporządkowane przez pole elektryczne i to uporządkowanie pozostało, i ono powoduje różnice współczynnika załamania dla różnych kierunków polaryzacji.

Ciekawostką jest fakt, że akurat tak się trafiło, że różnica dróg optycznych dla polaryzacji „szybszej” i „wolniejszej” w tym nożyku jest o pół długości fali (a może np. o półtora – wynik jest podobny, jakkolwiek bardziej kolorowy) – pewnie, jakby się chciało tak trafić celowo, to łatwo by się to nie udało, i może nożyki wyprodukowane innego dnia nie trafią tak dobrze z tą różnicą.

Nie wiemy, czy to jest różnica w całej objętości tworzywa, czy tylko blisko powierzchni – jeśli by była w objętości, to można by się spodziewać, że będzie zależeć od grubości nożyka, co powinno być łatwe do zaobserwowania (na ile ciemne stają różne miejsca nożyka, czy to zależy od grubości). Naprężenia, jeśli to one wprowadzają anizotropię, często są rozłożone dość nieregularnie – to powinno być widoczne (jest taki sposób badania rozkładu naprężeń, że element z przezroczystego tworzywa umieszcza się pomiędzy skrzyżowanymi polaryzatorami – tak, by światło nie przechodziło – i naciska się nań, aby spowodować naprężenia – na obrazie w polaryzatorze pojawiają się barwne prążki zagęszczające się tam, gdzie naprężenia są największe).