Moje pytanie dotyczy kwestii obserwacji astronomicznych. Wiadomo, że Wszechświat się rozszerza, a tempo jego ekspansji cały czas rośnie. Badacze potrafią określić odległości dzielące nas od odległych galaktyk, wiemy także ile czasu światło potrzebowało na dotarcie od nich do nas na Ziemię. Im dalszy obiekt obserwujemy, tym bardziej „nieaktualny” jego obraz widzimy. Obiekty oddalone od nas o 15 mld lat widzimy takimi, jakimi były właśnie owe 15 mld lat temu. A więc obserwując coraz odleglejsze obiekty oglądamy coraz młodszy Wszechświat. Z teorii wielkiego wybuchu wynika, że młody Wszechświat był mniejszy niż obecnie. Jak pogodzić to, że im dalej sięgamy w obserwacjach, musimy ogarniać coraz większą przestrzeń, z coraz większymi odległościami dzielącymi poszczególne obiekty, a jednocześnie widzimy Wszechświat coraz młodszy, który z definicji powinien być coraz mniejszy w miarę zbliżania się do momentu wielkiego wybuchu? Drugie pytanie wiąże się z pierwszym. Jeżeli ekspansja Wszechświata zaczęła się od bezwymiarowego punktu (początkowej osobliwości) i przebiegała od początku tak samo we wszystkich kierunkach, to jak to możliwe, że najstarsze obiekty są najbardziej od nas oddalone. Przecież w każdym możliwym układzie składającym się z dwóch obiektów oddalających się od siebie z jednego punktu przestrzeni (czyli z początkowej osobliwości) pod wpływem tej samej siły skierowanej w różne strony, ten „punkt początkowy” będzie znajdował się pośrodku, pomiędzy tymi obiektami. Innymi słowy najstarsza część Wszechświata powinna być widoczna nie najdalej od nas, ale pośrodku, pomiędzy nami, a najodleglejszymi obiektami. Jeżeli to rozumowanie jest poprawne, to wynika z niego, że miejsce, w którym znajdowała się początkowa osobliwość, powinno być w zasięgu naszych obserwacji.
Obserwacje astronomiczne a młody Wszechświat
Pytanie
Odpowiedź
Odpowiedzi na te pytania zostaną udzielone poprzez odwołanie się do modelu wszechświata, który jest na tyle prosty, że jego ewolucję można wiernie przedstawić na płaszczyźnie. W tym modelu przestrzeń jest jednowymiarowa i ma postać okręgu (mówiąc bardziej fachowo: ma topologię okręgu). Ewolucja tej przestrzeni polega na równomiernym przyroście jej długości, który zachodzi w ten sposób, że w chwili $t>0$ całkowita długość przestrzeni-okręgu wynosi $2\pi t$ (czas $t$ mierzymy tu w metrach: $1$ metr czasu to czas, w jakim światło w próżni przebywa odległość $1$ metra; dzięki takiemu wyborowi jednostek wielkość $2\pi t$ ma poprawny wymiar długości). Tak zdefiniowany model jest jednorodny i izotropowy — jednorodność oznacza, że w każdej chwili żaden punkt przestrzeni nie jest wyróżniony w stosunku do jej pozostałych punktów, a izotropowość oznacza, że w każdej chwili w każdym punkcie przestrzeni nie jest wyróżniony żaden kierunek (w naszym modelu w każdym punkcie mamy dwa przeciwne do siebie kierunki ponieważ przestrzeń jest tu jednowymiarowa).
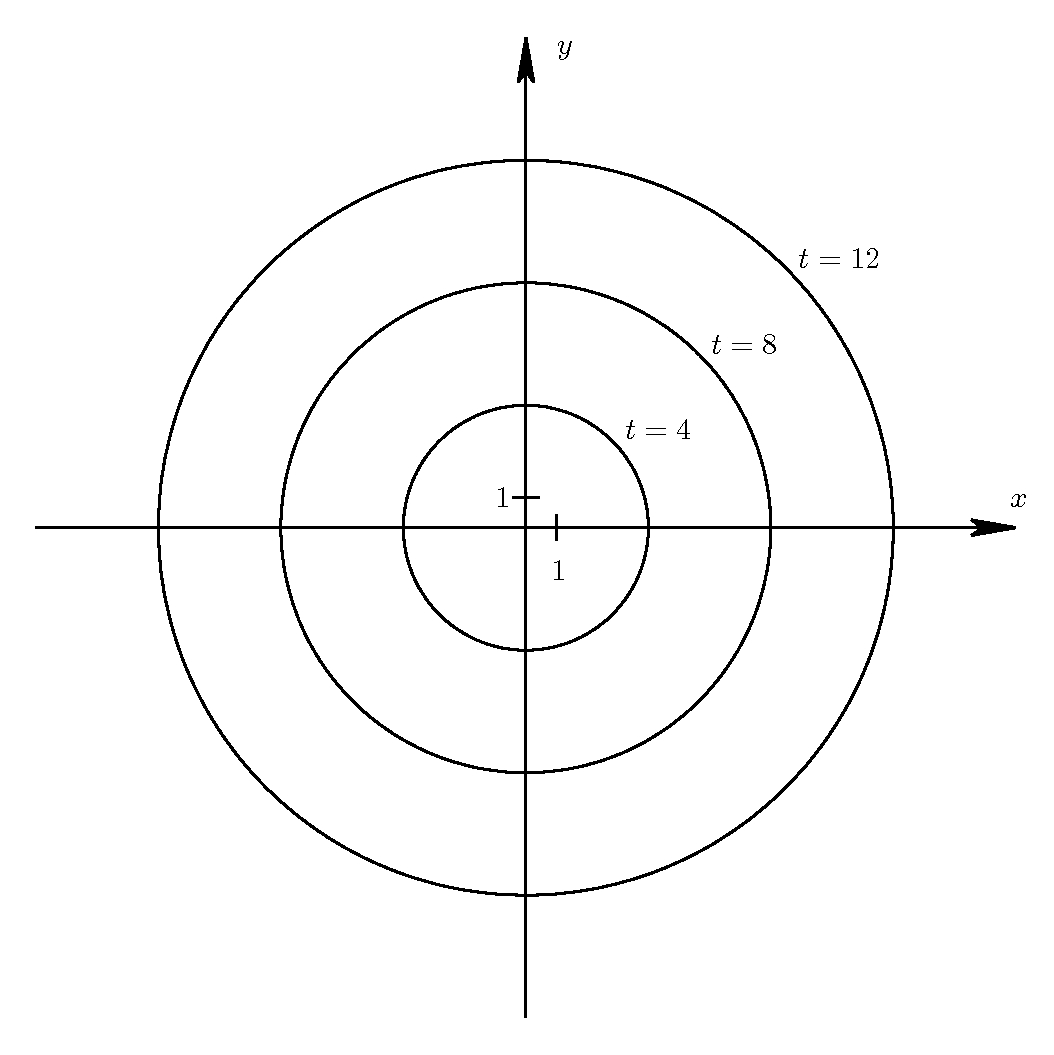
Rysunek 1
Przestrzeń naszego modelu w chwili $t$ możemy przedstawić w kartezjańskim układzie współrzędnych na płaszczyźnie jako okrąg o środku w punkcie $(0,0)$ i promieniu $t$ — na rysunku 1 widzimy tą przestrzeń w chwilach $t=4,8,12$. Czasoprzestrzeń naszego modelu to kolekcja przestrzeni we wszystkich chwilach $t>0$. Możemy ją więc zobrazować jako zbiór wszystkich okręgów o środku w punkcie $(0,0)$ i niezerowym promieniu. Oznacza to, że czasoprzestrzeń może być tu utożsamiona z płaszczyzną bez punktu $(0,0)$ (jako, że ten punkt nie należy do żadnego z rozważanych okręgów). Współrzędna czasowa $t$ danego zdarzenia rozumianego jako punkt $(x,y)\neq (0,0)$ na tej płaszczyźnie to standardowa odległość tego punktu od punktu $(0,0)$:
\[
t(x,y)=\sqrt{x^2+y^2}.
\]
Zatem współrzędna czasowa $t$ rośnie w kierunkach radialnych rozchodzących się z punktu $(0,0)$, co pokazane jest na rysunku 2.
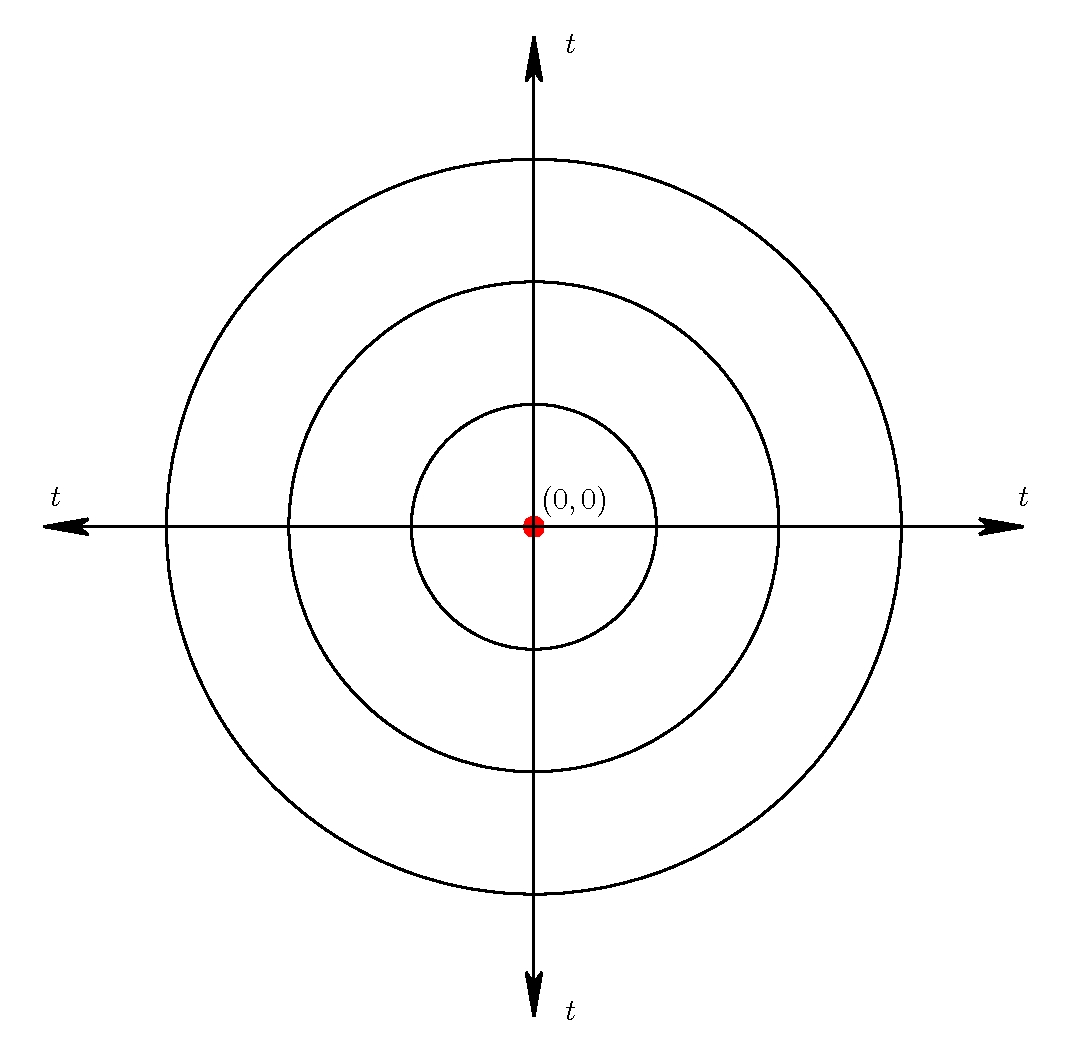
Rysunek 2
Odnosząc się do pierwszej części pytania trzeba zaznaczyć, że mówiąc o odległości obserwowanej galaktyki (czy innego obiektu) mamy zazwyczaj na myśli jej odległość od nas w chwili obecnej czyli w chwili obserwacji, a nie w chwili emisji światła, które w tym momencie dociera do nas z tej galaktyki. Zobaczymy poniżej jak ta obecna odległość zależy od chwili emisji.
W jednorodnych i izotropowych modelach wszechświata stanowiących podstawę współczesnej kosmologii linia świata danego obiektu jest krzywą w czasoprzestrzeni, która pokazuje, jak zmienia się położenie obiektu w czasie $t$. W tych modelach linie świata galaktyk są krzywymi, które w każdej chwili $t$ są ortogonalne do przestrzeni. W naszym modelu będą to półproste wychodzące z punktu $(0,0)$ — na rysunku 3 przykładowa linia świata galaktyki jest oznaczona symbolem $g$. Skoro obserwacje odległych galaktyk polegają na detekcji wysyłanego przez nie światła, to aby opisać zależność pomiędzy czasem emisji światła przez galaktykę a jej obecną odległością od obserwatora powinniśmy umieć opisać linie świata fotonów. Ponieważ w naszym modelu przestrzeń to okrąg o środku w punkcie $(0,0)$ więc możemy się spodziewać, że linia świata fotonu będzie obiegać ten środek. Ale ponieważ przestrzeń rozszerza się, więc ta linia powinna być pewnego rodzaju spiralą. Z obliczeń wynika, że linia świata fotonu jest w tym modelu odcinkiem spirali logarytmicznej — parametryczna postać takiej linii świata to
\[
[a,b]\ni\varphi\mapsto
\begin{pmatrix}
x(\varphi)\\
y(\varphi)
\end{pmatrix}=
\begin{pmatrix}
\exp(\alpha\varphi+\varphi_0)\cos\varphi\\
\exp(\alpha\varphi+\varphi_0)\sin\varphi
\end{pmatrix} \in \mathbb{R}^2,
\]
gdzie $\alpha=\pm 1$, a $\varphi_0$ jest dowolną stałą. Przykładowa linia świata fotonu jest oznaczona na rysunku 3 symbolem $f$.
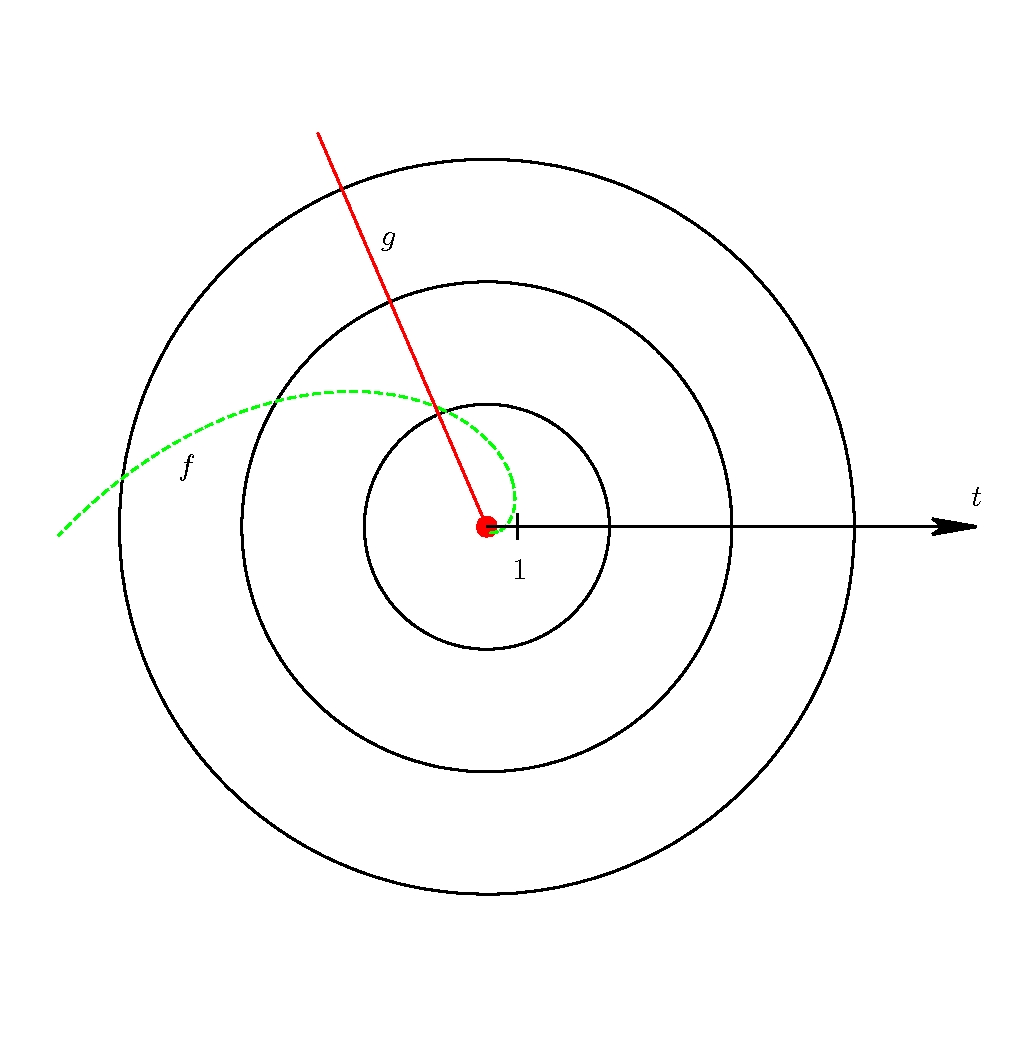
Rysunek 3
Rozważmy teraz galaktykę $g$, której linia świata przedstawiona jest na rysunku 4 jako pionowa półprosta oznaczona tym samym symbolem. Przypuśćmy, że w chwili $t=12$ do obserwatora $\cal O$ znajdującego się w tej galaktyce docierają z przeciwnych stron fotony wyemitowane przez dwie inne galaktyki $g_1$ i $g_2$. Detekcja tych fotonów przez obserwatora $\cal O$ jest zdarzeniem, które oznaczymy symbolem $Z$. Załóżmy dodatkowo, że galaktyka $g_1$ wyemitowała swoje fotony w chwili $t=8$ (zdarzenie $Z_1$), a galaktyka $g_2$ w chwili $t=4$ (zdarzenie $Z_2$). Aby znaleźć położenie galaktyki $g_1$ w momencie emisji światła musimy narysować linię świata fotonu kończącą się w punkcie $Z$ czasoprzestrzeni i zaczynającą się na okręgu $t=8$ (na rysunku 4 ta linia świata oznaczona jest symbolem $f_1$) — początek tej linii wyznacza zdarzenie $Z_1$. Linia świata galaktyki przechodząca przez to zdarzenie to linia świata galaktyki $g_1$. Podobnie postępując znajdujemy linię świata $f_2$ fotonów wysłanych przez galaktykę $g_2$, co pozwala nam określić położenie zdarzenia $Z_2$ oraz linię świata galaktyki $g_2$.
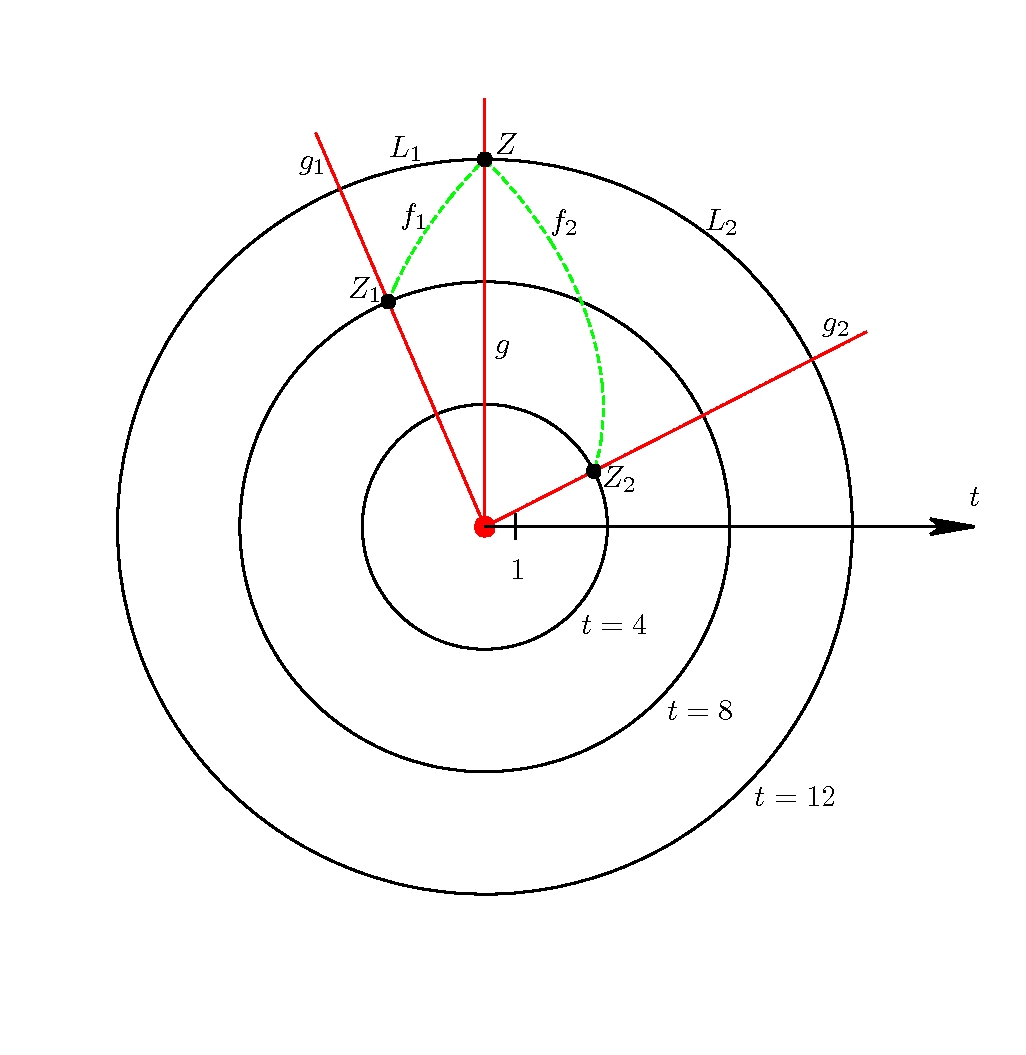
Rysunek 4
Chwila obserwacji galaktyk $g_1$ i $g_2$ przez obserwatora $\cal O$ to $t=12$. Przecięcie się linii świata galaktyki $g_1$ z okręgiem $t=12$ określa położenie galaktyki $g_1$ w tej chwili, a długość łuku tego okręgu pomiędzy tym położeniem a punktem $Z$ to odległość $L_1$ pomiędzy galaktyką $g_1$ a obserwatorem $\cal O$ w chwili obserwacji. Analogicznie wyznaczamy odległość $L_2$ pomiędzy obserwatorem a galaktyką $g_2$ w tej samej chwili.
Z rysunku 4 widać, że w chwili $t=12$ czyli w chwili obserwacji odległość $L_2$ pomiędzy obserwatorem $\cal O$ i galaktyką $g_2$, która wcześniej wyemitowała swoje fotony jest większa od odległości $L_1$ pomiędzy tym obserwatorem a galaktyką $g_1$, która swoje fotony wyemitowała później.
Dla ścisłości trzeba tu dodać, że w naszym modelu powyżej otrzymana zależność jest słuszna w przypadku tych fotonów, których linie świata pomiędzy emisją a detekcją wykonują nie więcej niż pół pełnego obiegu wokół punktu $(0,0)$. Dla linii świata nie spełniających tego warunku omawiana zależność może zostać zaburzona z powodu nietrywialnej topologii przestrzeni — ponieważ przestrzeń ta jest okręgiem, to np. fotony wysłane przez galaktykę $g$ w jednym kierunku mogą dotrzeć do niej z przeciwnej strony po dokonaniu pełnego obiegu przestrzeni-okręgu (wtedy obserwator $\cal O$ zobaczy przeszły obraz swojej własnej galaktyki). W tym przypadku w chwili obserwacji odległość między galaktyką wysyłającą fotony a galaktyką, w której dokonuje się obserwacji wynosi $0$. Widać stąd, że nietrywialna topologia przestrzeni może skomplikować prostą relację pomiędzy czasem emisji światła a obecną odległością źródła od obserwatora.
Odnośnie „miejsca, w którym znajdowała się osobliwość początkowa”: patrząc na rysunek 2 zmniejszajmy wartość współrzędnej czasowej $t$ aż do osiągnięcia wartości $0$. Co wtedy dzieje się z przestrzenią czyli z okręgiem? Równomiernie kurczy się do punktu $(0,0)$, który pełni tu rolę osobliwości początkowej. Odwracając kierunek zmian współrzędnej $t$ od $0$ do wartości dodatnich widzimy, że cała przestrzeń „wyłania” się z osobliwości początkowej. Zatem w tym sensie każdy punkt przestrzeni „pochodzi” z tej osobliwości i „miejscem, w którym znajdowała się osobliwość początkowa” jest cała przestrzeń.

