W materiałach antyferromagnetycznych sieć krystaliczna może być podzielona na dwie podsieci. W wysokich temperaturach momenty magnetyczne atomów leżących na tych podsieciach rozłożone są w losowych kierunkach i stąd układ zachowuje się jak typowy paramagnetyk. Poniżej pewnej temperatury krytycznej, zwanej temperaturą Neela, momenty magnetyczne, związane ze spinami, na obu podsieciach porządkują się ustawiając się antyrównolegle do tych na drugiej podsieci, jak widać na rysunku poniżej.
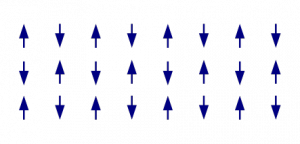
Źródło: https://en.wikipedia.org/wiki/Antiferromagnetism
W związku z tym, przy braku zewnętrznego pola magnetycznego momenty magnetyczne sąsiednich atomów kompensują się i układ jako całość nie wykazuje spontanicznego namagnesowania także w niskich temperaturach.
Zachowanie antyferromagnetyka w fazie uporządkowanej, który znajduje się w zewnętrznym polu magnetycznym, zależy od kierunku pola.
Jeśli pole jest prostopadłe do kierunku uporządkowania momentów magnetycznych to układ zachowuje się jak paramagnetyk, którego podatność magnetyczna słabo zależy od temperatury. Związane jest to z tym, że zewnętrzne pole wychyla lekko spiny w kierunku jego zwrotu i przez to nie są one już zwrócone całkowicie antyrównolegle. Powoduje to, że nie następuje całkowita kompensacja sąsiednich momentów i tym samym jest indukowane słabe niezerowe namagnesowanie próbki w kierunku pola zewnętrznego, które znika przy jego usunięciu.
Jeśli pole jest równoległe to odpowiedź układu jest bardziej skomplikowana. W temperaturze zera bezwzględnego momenty są zamrożone w antyrównoległych położeniach, które minimalizują energię całkowitą. Dla ustawienia idealnie równoległego siła działająca na momenty magnetyczne pochodząca od zewnętrznego pola jest zerowa. Dlatego podatność magnetyczna wynosi także zero, czyli układ nie reaguje na zewnętrzne pole magnetyczne. Jednak jeśli wartość zewnętrznego pola przekroczy wartość krytyczną, powyżej której energia oddziaływania pojedynczych spinów z zewnętrznym polem magnetycznym będzie większa niż energia wymiany między dwoma sąsiednimi spinami, która odpowiada za ich antyrównoległe ustawienie, to następuje natychmiastowe przestawienie spinów tak aby wszystkie były zwrócone w kierunku pola zewnętrznego i stąd układ zaczyna zachowywać się jak nasycony ferromagnetyk.
W skończonej temperaturze na skutek fluktuacji termicznych momenty magnetyczne drgają wokół położeń równowagi. W takich warunkach zewnętrzne pole magnetyczne będzie mogło odchylać spiny i układ będzie wykazywał niezerową podatność magnetyczną w kierunku równoległym, która rośnie wraz z temperaturą, aż do temperatury Neela. Oczywiście powyżej krytycznej wartości pola zewnętrznego układ znowu zachowuje się jak ferromagnetyk. Zależności podatności dla obu kierunków stają się identyczne w temperaturze Neela, powyżej której układ zachowuje się jak zwykły paramagnetyk.
Powyższe rozważania ilustruje wykres zależności podatności $\chi$ od temperatury $T$ odpowiednio dla kierunku równoległego $\chi_{\parallel}$ oraz prostopadłego $\chi_{\perp}$ do zewnętrznego pola.
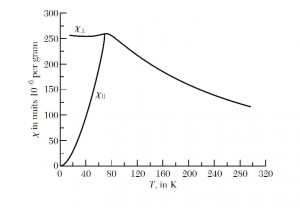
http://inspirehep.net/record/1293691/plots
Dotychczasowe rozważania tyczyły się przypadku idealnego kryształu, w którym faza antyferromagnetyczna tworzy jedną domenę. W rzeczywistych układach mamy często do czynienia z polikryształami lub materiałami gdzie spontanicznie faza antyferromagnetyczna dzieli się na liczne różnie względem siebie zorientowane domeny. W takiej sytuacji wypadkowa przenikalność jest izotropowa i zadana wzorem $\chi=\frac{1}{3}\chi_{\parallel}+\frac{2}{3}\chi_{\perp}$.
Stąd typowy antyferromagnetyk będzie zachowywał się jak słaby paramagnetyk o anomalnej zależności podatności i tym samym namagnesowania od temperatury. Ilustruje te wnioski poniższy wykres przedstawiający porównanie typowych zależności namagnesowania $M$ od natężenia zewnętrznego pola magnetycznego $H$ podstawowych rodzajów materiałów magnetycznych.
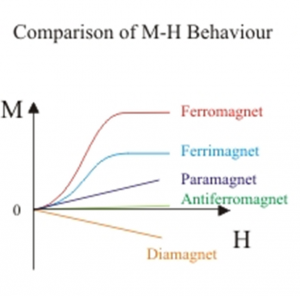
Źródło: http://nptel.ac.in/courses/113104005/81
Widać na nim, że namagnesowanie antyferromagnetyka jest najsłabsze ze wszystkich typów i dodatnie tak jak dla paramagnetyka i przeciwne niż dla diamagnetyka.




