Podczas uczenia się o ruchu przeczytałem, że chcąc obliczyć (z wykresu) drogę pokonaną przez ciało trzeba obliczyć pole figury zawartej pod wykresem. Na przykład gdy liczy się drogę z wykresu $v(t)$ w ruchu jednostajnie przyspieszonym, należy pomnożyć prędkość i czas oraz podzielić to na dwa (pole trójkąta). Moim pytaniem jest: dlaczego nie można użyć tutaj zwykłego wzoru na drogę ($s=v\cdot t$)? Gdy się go użyje powstaje rozbieżność (wynik jest wtedy dwa razy większy) wynikająca z tego że licząc pole figury dzieli się na dwa. Dlaczego tak się dzieje? Myślę, że jest to związane z przyspieszeniem, ponieważ licząc drogę z wykresu $v(t)$ w ruchu jednostajnym wystarczy policzyć już pole prostokąta ($a\cdot b=t\cdot v=s$).
Pole pod wykresem i całkowanie
Pytanie
Odpowiedź
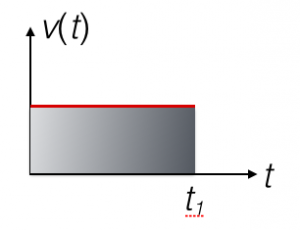
Wzór $s=v\cdot t$ jest słuszny tylko wtedy, kiedy dany obiekt porusza się ze stałą prędkością $v$, tzn. w każdej chwili czasu $t$ prędkość jest taka sama. Wykres $v(t)$ w takim wypadku wygląda następująco (wartość prędkości zaznaczona jest na czerwono):
i jeśli obiekt porusza się od chwili $t=0$ do chwili $t=t_1$, to przebyta $s$ droga odpowiada polu (szarego) prostokąta o bokach $t_1$ oraz $v$, tzn. $s=v t_1$.
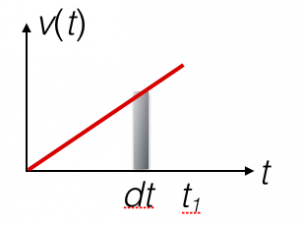
Jeśli obiekt nie porusza się ze stałą prędkością to sprawa jest bardziej skomplikowana. Wzoru $v\cdot t$ nie możemy użyć do znalezienia całkowitej przebytej drogi, gdyż prędkość $v$ nie jest stała. Możemy natomiast cały czas w którym odbywał się ruch podzielić na bardzo krótkie kawałki. W takim bardzo krótkim kawałku prędkość będzie w przybliżeniu stała — tzn. jeśli dany odcinek czasu będzie bardzo krótki, to będzie można zaniedbać zachodzące w nim zmiany prędkości. Załóżmy, że dany obiekt porusza się ze stałym przyspieszeniem $a$, czyli $v=a\cdot t$, i rozważmy krótki odcinek czasu o długości, którą oznaczymy $dt$. Wtedy, w przybliżeniu, droga przebyta podczas tego odcinka czasu dana jest przez pole bardzo wąskiego (szarego) prostokąta:
i wynosi $v\cdot dt$. W różnych (krótkich) odcinkach czasu przebyta droga będzie także (w przybliżeniu) dana przez pole takich prostokątów — natomiast rzecz w tym, że ich wysokości będą różne. Rozpatrując wiele prostokątów takich jak na rysunku powyżej, ale o różnych wysokościach, jako przebytą drogę otrzymamy pole trójkąta pod czerwoną krzywą.
Wykonajmy zatem dokładny rachunek w ruchu jednostajnie przyspieszonym. Cały czas ruchu $t_1$ podzielmy na $n$ części o długości $dt=t_1/n$ każda, zakładając przy tym, że każda z tych części jest bardzo krótka — tzn. $n$ jest bardzo dużą liczbą. Wszystkie te części możemy ponumerować zmienną $m$, która przyjmuje wartości od 1 do $n$, $m=1,…,n$. W chwili odpowiadającej numerowi $m$ prędkość obiektu wynosi $v=a \cdot m\, dt=a\cdot m\frac{t_1}{n}$ (gdyż obiekt poruszał się z przyspieszeniem $a$ przez całkowity czas $m\,dt$). Zatem w tym odcinku czasu obiekt przebędzie (w przybliżeniu) drogę $v\cdot dt = a\cdot m\frac{t_1^2}{n^2}$. Aby otrzymać całkowitą drogą należy dodać do siebie wszystkie takie krótkie kawałki drogi, dla wszystkich możliwych wartości $m$ (od 1 do $n$), czyli
$$
s = \sum_{m=1}^n a\cdot m\frac{t_1^2}{n^2} = a\cdot \frac{t_1^2}{n^2} \sum_{m=1}^n m = a\cdot \frac{t_1^2}{2} \frac{(n-1)n}{n^2},
$$
gdzie wykorzystaliśmy wzór $\sum_{m=1}^n m = \frac{(n-1)n}{2}$. Przyjmując wreszcie, że $n$ jest bardzo duże — czyli dążące do nieskończoności — ostatni ułamek dąży do wartości 1 (gdyż $\frac{(n-1)n}{n^2}=1 – \frac{1}{n}$, i dla dużych $n$ to co odejmujemy od jedynki staje się nieistotne). Otrzymujemy więc
$$
s = \frac{1}{2} a\cdot t_1^2,
$$
czyli rzeczywiście wzór na pole trójkąta.
Opisana powyżej operacja w istocie jest tzw. całkowaniem, a sumowanie po nieskończenie wielu elementach oznacza się symbolem $\int$, albo też$\int_{t_0}^{t_1}$ (chcąc podkreślić, że sumujemy wkłady w przedziale od $t_0$ do $t_1$). Zatem wzór na drogę można napisać następująco
$$
s=\int_{t_0}^{t_1} v(t)\, dt.
$$
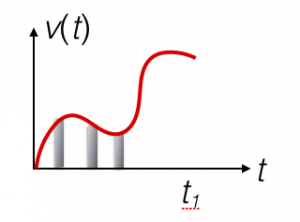
Wzór ten jest ważny dla dowolnej zależności $v(t)$, a przebyta droga jest zawsze równa polu pod wykresem funkcji $v(t)$ — które można interpretować jako sumę pól nieskończenie wielu nieskończenie cienkich prostokątów (czyli właśnie „całkę) — tak jak np. dla takiej funkcji, z kilkoma przykładowymi takimi prostokątami zaznaczonymi na szaro (z konieczności narysowanymi jako o skończonej szerokości, i o różnych wysokościach):