Satelity nie poruszają się sinusiodalnie względem Ziemi, lecz krążą wokół naszej planety po orbitach kołowych lub eliptycznych. Natomiast jeżeli na siatce współrzędnych geograficznych zaznaczymy te punkty znajdujące się na powierzchni Ziemi, nad którymi przelatuje dany satelita, to otrzymamy krzywą, która w pewnych szczególnych przypadkach może przypominać sinusoidę.

W rzeczywistości ta krzywa w istotny sposób różni się od sinusoidy. Aby ją opisać oznaczmy symbolem $\alpha$ szerokość geograficzną, a symbolem $\beta$ długość geograficzną – obie wielkości rozumiane są tu jako kąty mierzone w radianach. Wtedy rozważana krzywa otrzymana dla satelity krążącego po orbicie kołowej może być opisana parametrycznie w następujący sposób:
\begin{equation}
\begin{aligned}
\alpha(t)&={\rm arcsin}(\sin\gamma \sin t), &&\\
\beta(t)&={\rm arctg}(\cos\gamma \,{\rm tg}\,t)+k\pi-at, & t&\in\, ]-\frac{\pi}{2}+k\pi,\frac{\pi}{2}+k\pi[\,,
\end{aligned}
\label{krz}
\end{equation}
gdzie $t$ jest parametrem, $k$ przebiega zbiór liczb całkowitych, $0\leq \gamma\leq \pi/2$ jest kątem nachylenia płaszczyzny orbity satelity do płaszczyzny równika Ziemi, a $|a|>0,059$ jest ilorazem okresu obiegu satelity wokół Ziemi przez okres obrotu Ziemi wokół swojej osi (wartość $a$ może być dodatnia lub ujemna, co odpowiada dwóm kierunkom obiegania Ziemi po tej samej orbicie). Dodajmy jeszcze, że kąty mierzone w radianach opisujące długość geograficzną zawierają się w przedziale $[-\pi,\pi]$, a jeżeli wartość funkcji $\beta(t)$ do tego przedziału nie należy, to utożsamiamy ją z kątem $\beta\in[-\pi,\pi]$ takim, że $\beta(t)-\beta=2\pi n$ dla pewnej całkowitej liczby $n$.

Na zamieszczonych poniżej rysunkach przedstawione są przykłady krzywej \eqref{krz} różniące się wartościami parametrów $\gamma$ i $a$. Na tych rysunkach długość i szerokość geograficzna zostały opisane standardowo czyli za pomocą stopni, a nie radianów. Przy opisach rysunków kąt $\gamma$ również będzie podawany w stopniach.

Na rysunku 1 widzimy krzywą otrzymaną dla satelity, którego orbita jest nachylona do równika pod kątem $15^\circ$, a okres obiegu wokół Ziemi to $2,4$ godziny ($a=0,1$). W tym wypadku otrzymana krzywa rzeczywiście przypomina sinusoidę.

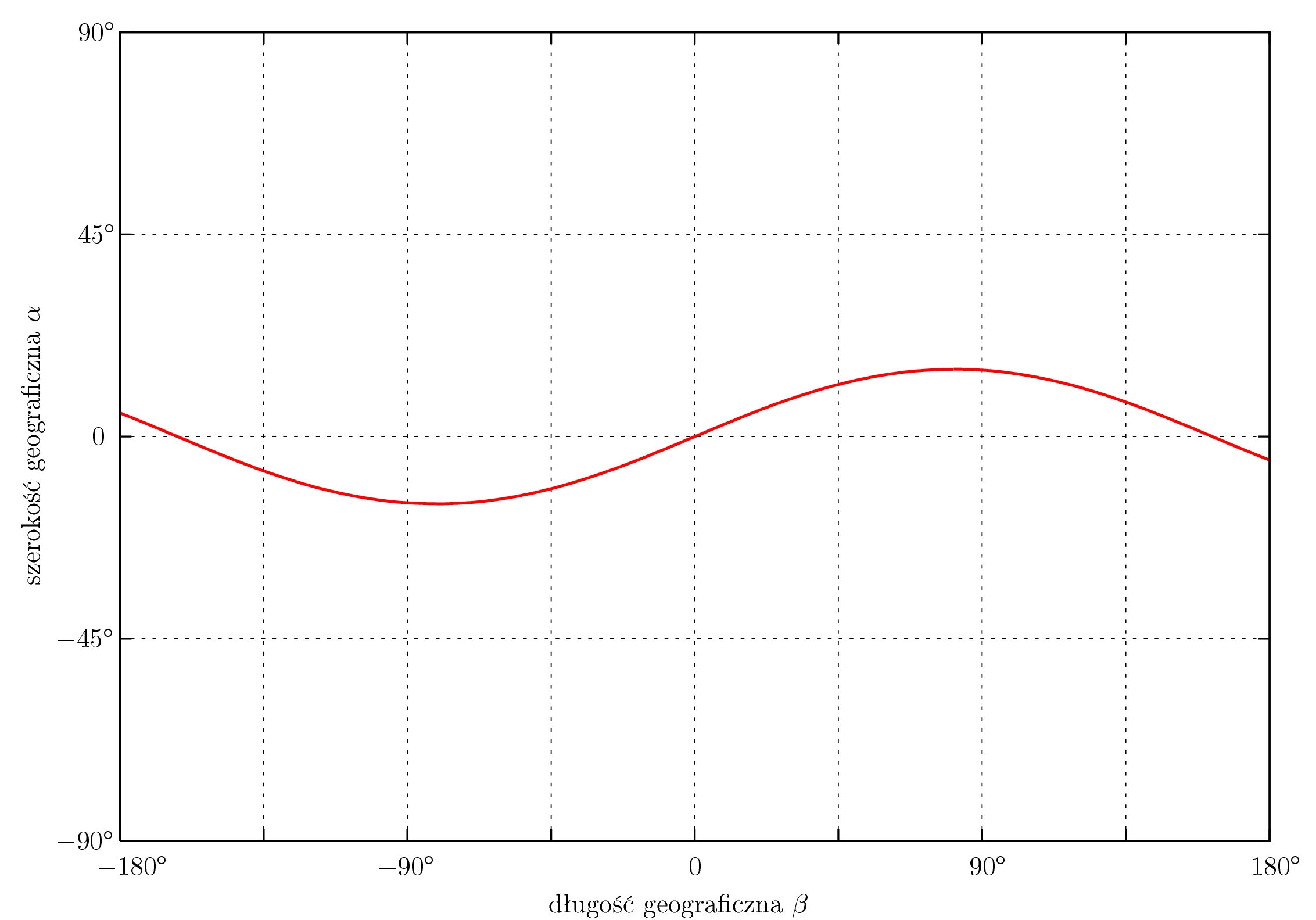
Rysunek 1

Jeżeli powiększymy nachylenie orbity satelity z poprzedniego przykładu do $85^\circ$ nie zmieniając okresu obiegu to zakreślana przez niego krzywa będzie wyglądać tak jak na rysunku 2:

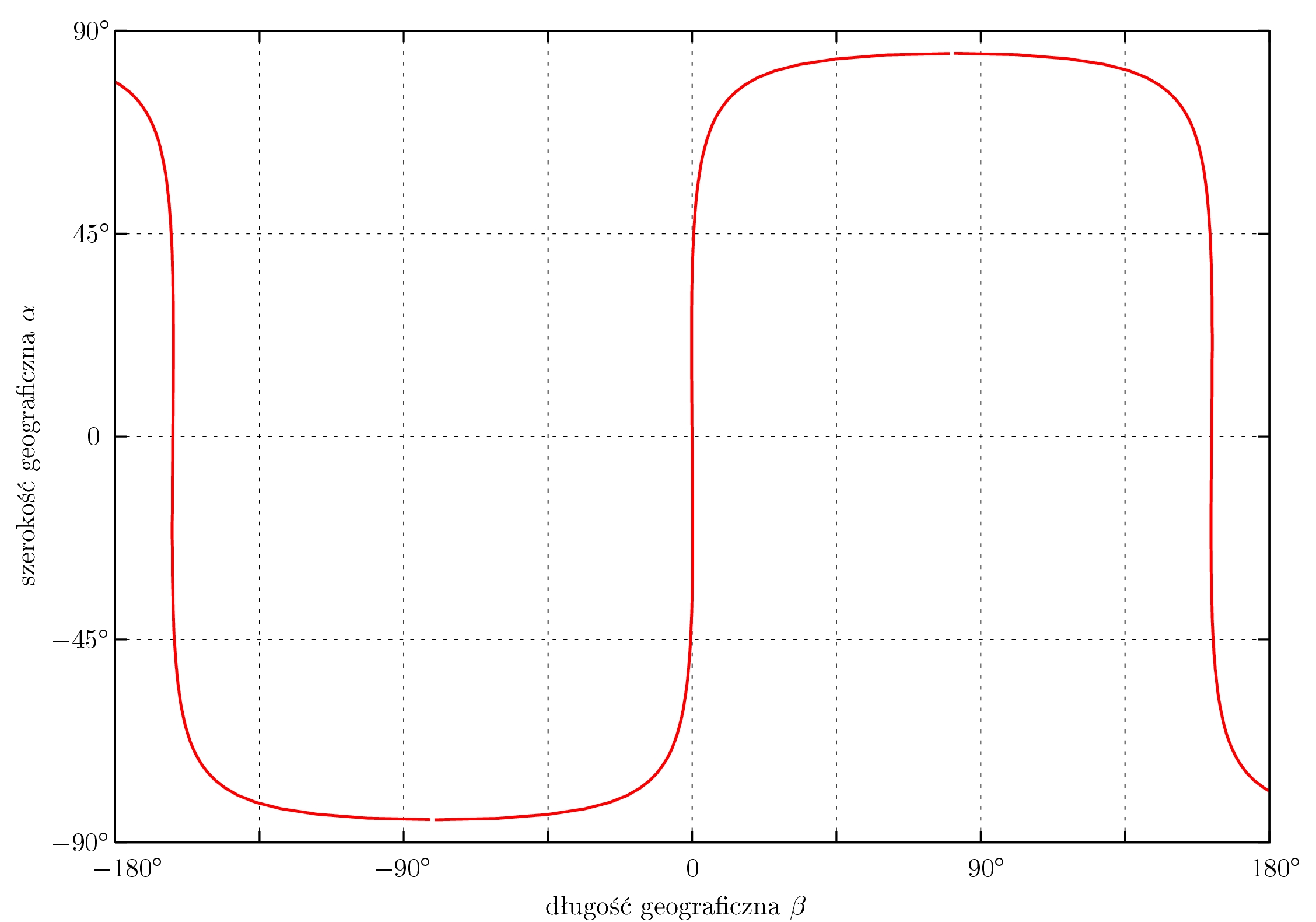
Rysunek 2

Rysunek 3 przedstawia krzywą zadaną przez satelitę, którego orbita jest nachylona do płaszczyzny równika pod kątem $60^\circ$ i który obiega Ziemię w ciągu $24$ godzin ($a=1$):

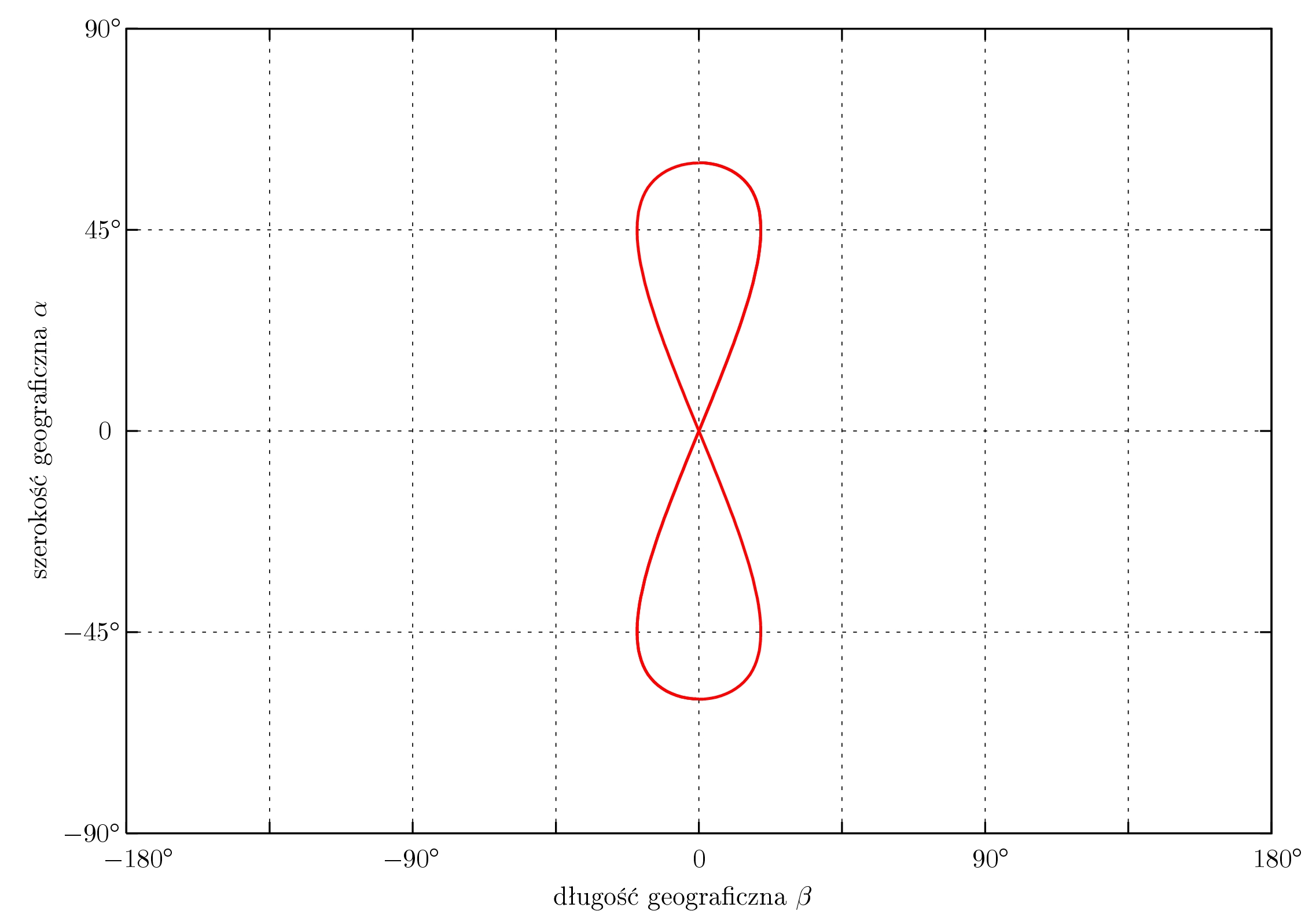
Rysunek 3

Na rysunku 4 widzimy krzywą otrzymaną dla kąta $\gamma=75^\circ$ i parametru $a=2$ (okres obiegu równy $48$ godzinom):

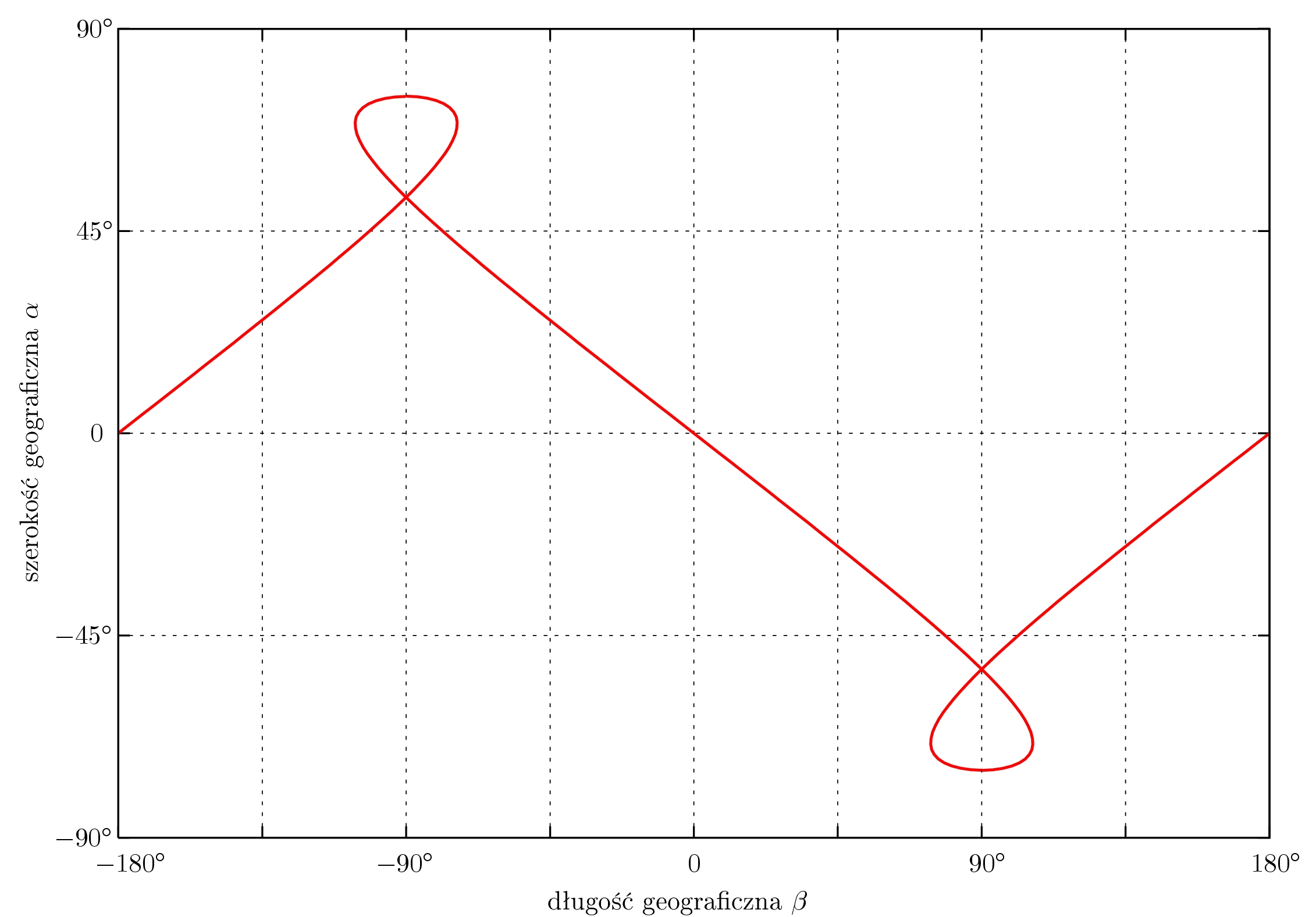
Rysunek 4