Z pojęciem entropii najczęściej mamy do czynienia w dwóch działach fizyki/matematyki:

• w teorii informacji
• w termodynamice i mechanice statystycznej

Żeby zastanowić się jaką jednostkę powinna mieć entropia, warto rozważyć kontekst, w którym zamierzamy ją wykorzystać. Rzućmy okiem na wykorzystanie jej w teorii informacji. Rozpatrzmy taki nieco dziwny przykład, który ilustruje mniej więcej to, co charakteryzuje entropia:

Gramy w grę, a nasza plansza wygląda w ten sposób: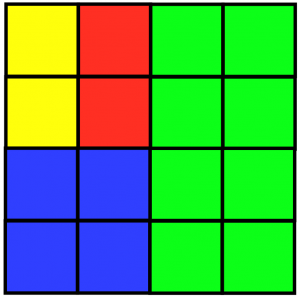A sama gra jest bardzo prosta. Ja jako pierwszy gracz zamykam oczy i palcem kiwam sobie nad planszą dopóki nie powie Pan „stop” (Pan nie widzi tego jak kiwam palcem, plansza jest na razie przed Panem ukryta). Po tym otwieram oczy i patrzę jaki kolor mi mój palec „wylosował” (tak, że np. prawdopodobieństwo tego że zatrzymał się na polu zielonym wynosiła 1/2). Teraz Pana zadaniem jest w jak najmniejszej ilości pytań dowiedzieć się, który z obszarów wylosowałem.

Okazuje się, że najlepsza strategia składałaby się z takich pytań:

1. Czy wylosowany obszar znajduje się od połowy na prawo? (jeśli odpowiem TAK to odgadł już Pan na pierwszym pytaniu! W końcu tylko zielony obszar znajduje się na prawo od środka. Jeśli odpowiem NIE to do wyboru jest jeszcze kilka opcji..)
   
2. Następne pytanie mogłoby dawać informację czy wylosowany obszar znajduję się poniżej białej kreski, tak jak poniżej:
   tutaj jest znowu podobna sytuacja jak wcześniej: jeżeli odpowiem TAK, to na drugim pytaniu gra się kończy, bo wylosowałem niebieski obszar, ale jeśli nie, to ostatnie pytanie powinno być już decydujące.
3. Tak samo jak wcześniej: czy wylosowany obszar znajduje się na lewo od prawej kreski?
   Niezależnie od tego co teraz odpowiem, gra się zakończy na trzecim pytaniu.

Widzimy więc, że czasami do zakończenia gry potrzebujemy 1,2 lub 3 pytania. Zatem, tak średnio, po ilu pytaniach by się gra skończyła? Tzn., grając np. 100 gier, ciekawi nas ile pytań było zadanych w ciągu tych gier, tę liczbę pytań dzielimy na 100, i otrzymujemy średnią liczbę pytań zadaną w każdej grze. Właśnie tę liczbę nazywamy entropią (w tym kontekście) – jest to oczekiwana liczba pytań, których się spodziewamy, żeby gra się zakończyła!

Korzystając z powyższej definicji policzmy dla naszego przykładu oczekiwaną liczbę pytań:
1. Prawdopodobieństwo tego, że 1 pytanie wystarczy wynosi 1/2 (co odpowiada sytuacji w której mój palec zatrzymał się na zielonym obszarze, a robi to właśnie z takim prawdopodobieństwem).
2. Prawdopodobieństwo tego, że 2 pytania wystarczą wynosi 1/4 (tutaj mój palec musiałby wylądować na obszarze niebieskim, który stanowi 1/4 całości).
3. Prawdopodobieństwo tego, że 3 pytania wystarczą wynosi 1/8 tutaj (mój palec musiałby wylądować na obszarze żółtym lub czerwonym).

Podsumowując, oczekiwana liczba zadanych pytań wynosi:
\[H = \frac{1}{2}\cdot 1 +\frac{1}{4}\cdot 2 + \frac{1}{8}\cdot 3  + \frac{1}{8}\cdot 3 = 1,75 \,\textrm{bits} \]
Entropię często nazywa się „zawartością informacji”. W naszym kontekście informacją są pytania, i to nie byle jakie pytania, a takie na które możemy odpowiedzieć jedynie TAK lub NIE – czyli trochę jak 1 i 0. Stąd jednostką informacji są bity. Zatem entropia takiego systemu (gry) wynosi 1,75 bitów. Ten opis można uogólnić na bardziej skomplikowane przypadki, bowiem widzieliśmy, że liczba zadanych pytań zależy wyłącznie od prawdopodobieństwa z jakim wylosuję dany obszar (np. dla 1/2 było 1 pytanie, 1/4 były 2 pytania itd.). Mając więc jakieś prawdopodobieństwo wylosowania 1, 2, 3,.. i $n$-tego obszaru mielibyśmy sumę:

\[H = p(1) \log_2 \frac{1}{p(1)} + p(2) \log_2 \frac{1}{p(2)} + p(3) \log_2 \frac{1}{p(3)} + … + p(n) \log_2 \frac{1}{p(n)} \]

Przechodząc do fizyki statystycznej – opis matematyczny jest analogiczny do tego powyżej, jednak interpretacja fizyczna jest zdecydowanie inna. W bardzo uproszczonym obrazie powiedzmy, że mamy jedną cząsteczkę uwięzioną w takim pojemniku dwuwymiarowym (cząsteczka jest nieruchoma):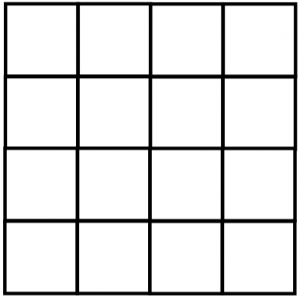Powiedzmy, że taka cząsteczka zajmuje 1 kwadrat na szablonie powyżej (jest to tzw. mikrostan). Każdy kwadrat może być zajęty z takim samym prawdopodobieństwem (jest to istotny postulat fizyki statystycznej). Teraz nasza sytuacja sprowadza się dokładnie do takiej samej jak w grze powyżej. Możemy śmiało zapisać:

\[S =k_B \Big(\frac{1}{16}\cdot \ln \frac{1}{16}+…+\frac{1}{16}\cdot \ln \frac{1}{16} \Big) = k_B\cdot\ln \frac{1}{16}\]

Jeżeli chodzi o jednostkę to jest ona taka sama jak jednostka stałej stojącej przed logarytmem, czyli tzw. stałej Boltzmanna $k_B$, która wyrażona jest w dżulach na kelvin (J/K). Jest ona tutaj po to, żeby wyprowadzenia z fizyki statystycznej niejako prowadziły nas do tożsamych wyrażeń uzyskanych za pomocą termodynamiki, tak żeby te dwa opisy były ze sobą spójne. Tak tylko na marginesie dodam, że powyższy opis entropii jako efektywne „liczenie zawartości informacyjnej po wszystkich mikrostanach układu” nazywamy entropią Gibbsa.

Więcej o entropii w kontekście teorii informacji można znaleźć w takim filmie, a w kontekście fizyki statystycznej tutaj i tutaj.