Mechanizm odpowiedzialny za to, że Księżyc (a także sztuczne satelity Ziemi) nie spada na naszą planetę najłatwiej jest chyba objaśnić na przykładzie satelity krążącego wokół Ziemi po orbicie w kształcie okręgu, którego środek pokrywa się ze środkiem Ziemi.

Podczas ruchu tego satelity jego odległość od środka Ziemi nie zmienia się – jest ona cały czas równa długości promienia orbity. Zatem aby wyjaśnić, dlaczego rozważany satelita nie spada na Ziemię wystarczy wyjaśnić, dlaczego pomimo przyciągania Ziemi odległość pomiędzy jej środkiem a satelitą pozostaje stała w czasie.

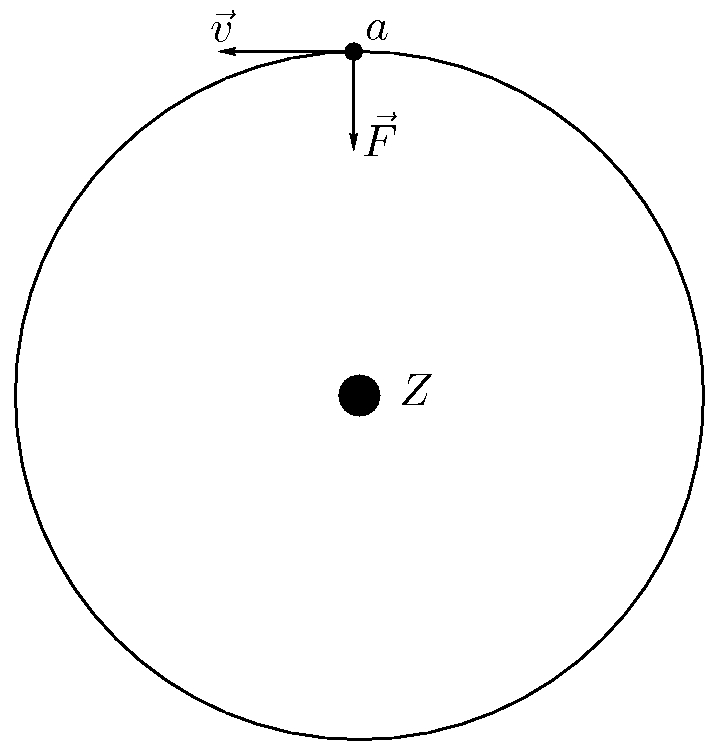
Na rysunku 1 widzimy satelitę znajdującego się w punkcie $a$ swojej orbity, siłę $\vec{F}$, z jaką Ziemia działa na satelitę oraz jego chwilową prędkość $\vec{v}$.

Rysunek 1

Siła $\vec{F}$ przyciągania grawitacyjnego jest wektorem o kierunku wyznaczonym przez promień orbity wyprowadzony z punktu $a$ i zwrocie ku Ziemi. Prędkość $\vec{v}$ jest wektorem stycznym do orbity, a ponieważ ta jest okręgiem więc prędkość $\vec{v}$ jest prostopadła do wspomnianego promienia i tym samym prostopadła do siły $\vec{F}$. Zastanówmy się teraz, jaką rolę w ruchu satelity odgrywają siła $\vec{F}$ i prędkość $\vec{v}$.

W oczywisty sposób przyciągająca siła $\vec{F}$ dąży do zmniejszenia odległości pomiędzy satelitą a Ziemią – gdyby prędkość $\vec{v}$ była równa zeru to satelita zacząłby spadać na Ziemię wzdłuż odcinka łączącego punkt $a$ i środek Ziemi.

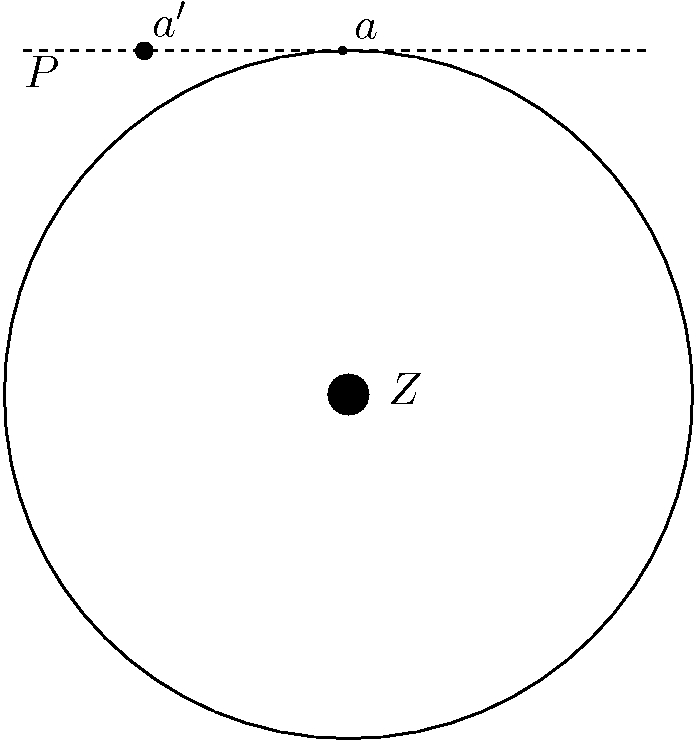
Gdyby z kolei siła $\vec{F}$ była równa zeru, to satelita posiadający niezerową prędkość $\vec{v}$ poruszałby się wzdłuż prostej $P$ stycznej do orbity zaznaczonej na rysunku 2 linią przerywaną i po upływie pewnego czasu znalazłby się w punkcie $a’$.

Rysunek 2

Zauważmy teraz bardzo istotną rzecz: otóż punkt $a’$ leży na zewnątrz orbity i w konsekwencji jest bardziej oddalony od środka Ziemi niż punkt $a$ znajdujący się na orbicie. Zatem niezerowa prędkość $\vec{v}$ oznacza tendencję satelity do poruszania się wzdłuż prostej stycznej $P$ i zarazem do oddalania się od Ziemi.

W przypadku rozważanego satelity mamy więc do czynienia z dwiema tendencjami:

• tendencją do zbliżania się do Ziemi, za którą odpowiedzialna jest siła przyciągania $\vec{F}$ oraz
• tendencją do oddalania się od Ziemi, za którą odpowiedzialna jest prędkość $\vec{v}$ prostopadła do siły $\vec{F}$.

Co więcej, relacja pomiędzy wartością prędkości $\vec{v}$ satelity i wartością siły $\vec{F}$ jest taka, że te dwie sprzeczne tendencje dokładnie się równoważą. W rezultacie satelita nie zmienia swej odległości od środka Ziemi, a jedynie swoje położenie na orbicie.

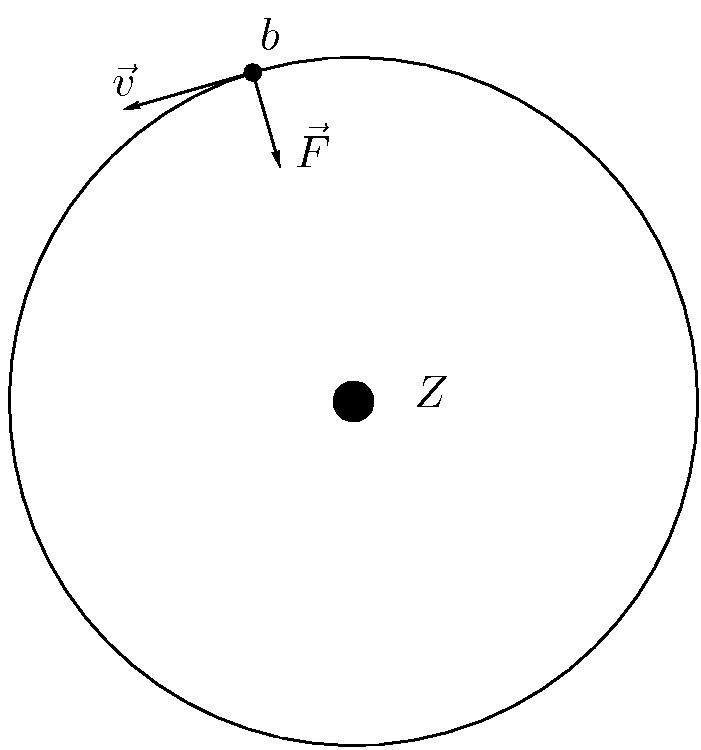
Na rysunku 3 satelita pokazany jest w nowym położeniu $b$ – tutaj jest on przyciągany ku Ziemi siłą $\vec{F}$ o tej samej wartości co poprzednio, a jego prędkość $\vec{v}$ o niezmienionej wartości jest styczna do orbity i tym samym prostopadła do siły $\vec{F}$ (prędkość satelity w punkcie $a$ różni się od jego prędkości w punkcie $b$ jedynie kierunkiem, a zmiana kierunku prędkości jest oczywiście wynikiem działania siły $\vec{F}$). Zatem w punkcie $b$ tak samo jak w punkcie $a$ występują dwie równoważące się tendencje: jedna do zbliżania się satelity do Ziemi i druga do oddalania się satelity od naszej planety.

Rysunek 3

Podsumowując: satelita na orbicie w kształcie okręgu pozostaje w stałej odległości od środka Ziemi dzięki temu, że

• jego prędkość jest prostopadła do siły przyciągania między satelitą a Ziemią,
• wartość prędkości jest odpowiednio skorelowana z wartością siły.

Wracając do Księżyca: jego orbita nie jest okręgiem o środku pokrywającym się ze środkiem Ziemi. Dlatego też odległość Księżyca od środka Ziemi nie pozostaje stała, lecz zmienia się w pewnym zakresie od najmniejszej w punkcie zwanym perygeum do największej w punkcie zwanym apogeum. Prędkość Księżyca nie jest w ogólności prostopadła do siły przyciągania pomiędzy nim a Ziemią, ale prędkość ta posiada niezerową składową prostopadłą do tej siły i ta niezerowa składowa jest odpowiedzialna za to, że Księżyc nie spada na Ziemię.

P.S. Bardziej zwięzłej odpowiedzi na to pytanie udzieliliśmy tutaj.