Wymienione wyżej metody mają zastosowanie nie tylko do obliczeń związanych ze stanem podstawowym atomów. Powszechnie wykorzystuje się je również do analizy stanów wzbudzonych oraz systemów bardziej skomplikowanych – molekuł. Są to informacje istotne, o czym przekonamy się niżej.

Energia wzbudzenia i przejścia 

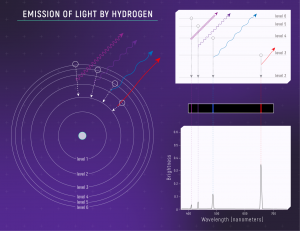
Rysunek 1. Emisja światła przez atom wodoru. Schemat przedstawia (1) atom wodoru (2) związek długości fali wyemitowanego światła z danym przejściem (3) ilustrację widma emisyjnego (4) wykres widma. Kliknij, aby powiększyć. Autor: NASA, ESA, Leah Hustak (STScI)

1. Interpretacja widma
   Zgodnie z postulatem wprowadzonym przez Bohra, atom może pochłonąć lub wyemitować jedynie taki foton, którego energia równa jest różnicy energii dwóch wybranych stanów. Oznacza to, że linie emisyjne uzyskane w trakcie pomiarów (schematycznie przedstawione na Rysunku 1 jako kolorowe linie na czarnym tle) odpowiadają właśnie różnicom energetycznym poziomów. Ale których poziomów? Aby odpowiedź na to pytanie choćby w przybliżony sposób, potrzebujemy obliczyć wartości energii poszczególnych stanów, a następnie porównać ich różnice z uzyskanym widmem.
2. Porównanie teorii z doświadczeniem
   Wyobraźmy sobie, że wyżej wspomniane obliczenia przeprowadziliśmy niezmiernie dokładnie. Co więcej, nasi koledzy i koleżanki z fizyki doświadczalnej również dopięli wszelkich starań, aby ich pomiary były równie dokładne. Porównujemy nasze wyniki i… uzyskujemy rozbieżność. Co może to oznaczać? Po pierwsze to sygnał, że być może nasza teoria jest błędna lub niekompletna (dobrymi przykładem jest tu np. przesunięcie Lamba). Współcześnie takim testom poddawane są raczej najprostsze układy i najbardziej zaawansowane teorie (np. elektrodynamika kwantowa); niemniej, warto o tym wspomnieć. Drugą możliwością jest błąd przy pomiarze. Słynnym przykładem są obliczenia dla molekuły wodoru wykonane w latach 60. przez Włodzimierza Kołosa i Lutosława Wolniewicza. Początkową rozbieżność z danymi doświadczalnymi próbowano skorygować kolejnymi poprawkami; doprowadziło to jednak do sytuacji, w której dokładność obliczeń przerosła możliwości eksperymentalne, a niezgodność pozostała obecna. Zmotywowało to Gerharda Herzberga (późniejszego noblistę) do powtórzenia swoich pomiarów. Jak można się domyślić, wymagały korekty.
3. Planowanie doświadczeń
   Fizyka ultrazimna zajmuje się układami schłodzonymi do temperatur niewiele wyższych od zera bezwzględnego. Jedną z metod używanych do osiągnięcia tak ekstremalnych warunków jest chłodzenie laserowe, którego powodzenie zależne jest od struktury energetycznej atomu czy molekuły. Dzięki obliczeniom teoretycznym jesteśmy w stanie zbadać, czy zaproponowany przez nas pierwiastek lub związek ma szansę sprawdzić się w tej procedurze.

Od strony bardziej technicznej można również wspomnieć, że znajomość energii atomów wykorzystywana jest jako jeden z pierwszych kroków do obliczeń dla innych układów. Przykładowo: dla danego stanu molekularnego uzyskujemy wartość energii $E$ jako funkcję odległości $R$ między atomami A i B. Aby dowiedzieć się, ile wynosi np. energia potrzebna do dysocjacji cząsteczki na dwa wolne atomu, konieczna jest znajomość krzywej oddziaływania $V(R)$. Zgodnie z intuicją można przyjąć, że energia oddziaływania będzie równa różnicy energii molekuły na danej odległości międzyatomowej i dwóch wolnych atomów, co sprowadza zagadnienie do obliczenia $V(R)=E_{AB}(R)-E_A-E_B$. W praktyce obliczeniowej powyższy wzór jest lekko modyfikowany ze względu na tzw. błąd superpozycji bazy, jednak nie redukuje to konieczności znajomości energii atomów. Warto mieć jednak świadomość, że w niektórych metodach (np. metodzie oddziaływania konfiguracji CI) energia molekuły w nieskończoności nigdy nie będzie równa sumie energii dwóch wolnych atomów; należy wtedy skorzystać bezpośrednio z wartości energii molekularnej na bardzo dużej odległości (np. 200 bohrów).