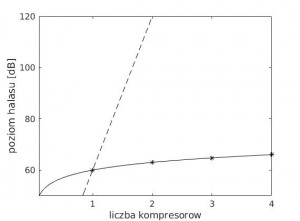
Po włączeniu drugiego kompresora hałas wzrośnie, ale tylko o około 3dB, czyli do około 63dB. Ma to związek ze sposobem w jaki ludzkie ucho rejestruje natężenie dźwięku. Dwa razy większe natężenie nie oznacza dwukrotnie większego poziomu hałasu. Poziom hałasu wprawdzie rośnie wraz z ilością włączonych urządzeń, ale nie jest to wzrost liniowy, a logarytmiczny. Funkcja logarytmiczna rośnie szybko dla małych wartości argumentu, ale później „wypłaszcza się”. Ilustruje to rysunek poniżej. Funkcja logarytmiczna określająca poziom hałasu zaznaczona jest na nim linią ciągłą. Poziomy hałasu dla 1, 2, 3 i 4 kompresorów wynoszą (w pewnym przybliżeniu) odpowiednio 60, 63, 64.8 i 66 dB. Dla porównania na rysunku zaznaczona jest również linią przerywaną funkcja liniowa. Jak widać przebiegi obu funkcji znacznie się różnią, a poziom hałasu rejestrowany przez ludzkie ucho po włączeniu obu kompresorów nie wzrośnie do 120dB, ale raczej pozostanie na poziomie bliskim 60dB.

Dokładniejsze obliczenia i wzory opisujące zjawisko zamieszczone są poniżej.

Poziom hałasu mierzony w decybelach związany jest z natężeniem dźwięku mierzonym w W/m² następującym wzorem

β=10log₁₀(I/I₀),

gdzie I jest poziomem natężenia dźwięku, a I₀  progiem słyszalności – ucho ludzkie nie zarejestruje dźwięków o natężeniu niższym niż I₀.

Jeden kompresor generuje hałas na poziomie 60dB. Podstawiając do wzoru otrzymujemy

60=10log₁₀(I₁/I₀),

gdzie I₁  jest wartością natężenia dźwięku generowanego przez kompresor.

Jeśli przyjmiemy, że częstotliwości fal dźwiękowych generowanych przez oba urządzenia są w danej chwili różne (w praktyce tak jest najczęściej), to natężenie generowane przez dwa urządzenia wyniesie 2I_1. Wówczas

β=10log₁₀(2I₁/I₀)=10log₁₀(I₁/I₀)+10log₁₀(2) = 60 + 10log₁₀(2) ≈ 60+3.01=63 dB,

czyli po włączeniu drugiego kompresora poziom hałasu wzrośnie o około 3dB.