Paradoks bliźniąt

Odpowiedź na powyższe pytanie będzie udzielona w oparciu o szczególną teorię względności.

Paradoks bliźniąt nie jest tak naprawdę paradoksem, a jedynie czasoprzestrzennym odpowiednikiem pewnego oczywistego faktu znanego każdemu z życia codziennego.

Otóż wyobraźmy sobie, że musimy np. odbyć podroż samochodem z Warszawy do Białegostoku. Przypuśćmy też, że zależy nam na oszczędności czasu i benzyny. Czy w tej sytuacji wyruszymy trasą S8 wybiegającą z Warszawy w kierunku północno-wschodnim ku Białemustokowi  czy raczej pojedziemy najpierw w kierunku południowo-wschodnim drogą nr 17 do Lublina, aby potem skręcić na północ i drogą nr 19 dojechać do Białegostoku?

Odpowiedź na powyższe pytanie jest oczywista, a jej oczywistość bierze się stąd, że każdy doskonale wie, że jeżeli z jednego miasta do drugiego prowadzą różne drogi to nie muszą mieć one takiej samej długości — w tym wypadku wystarcza rzut oka na mapę Polski, aby przekonać się, że długość trasy S8 pomiędzy Warszawą i Białymstokiem jest znacznie mniejsza niż długość trasy utworzonej z dróg 17 i 19, która to trasa również łączy te dwa miasta.

Podobnie, jeżeli w trójwymiarowej przestrzeni ustalimy dwa punkty $a$ i $b$ i połączymy te punkty różnymi krzywymi (rysunek 1) to dla nikogo nie będzie zaskoczeniem, jeśli się okaże, że te krzywe mają różną długość. Co więcej, dowodzi się, że spośród wszystkich krzywych łączących ustalone punkty $a$ i $b$ najkrótszą krzywą jest odcinek linii prostej zadany przez te dwa punkty.

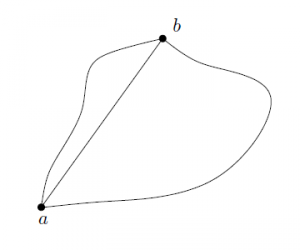Rysunek 1: Krzywe różnej długości łączące ustalone punkty $a$ i $b$.

Okazuje się, że w przypadku paradoksu bliźniąt mamy do czynienia z analogiczną sytuacją. Aby opisać tą analogię wyobraźmy sobie obserwatora inercjalnego, który obserwuje ruch wybranego ciała i każdej chwili $t$ przypisuje współrzędne $(x,y,z)$ miejsca, w którym to ciało znajdowało się w tej chwili. W ten sposób powstaje funkcja

\[
t\mapsto \big(x(t),y(t),z(t)\big)
\]

opisująca ruch obserwowanego ciała.

Powyższą funkcję można przedstawić w postaci wykresu na czterowymiarowym diagramie czasoprzestrzennym tak jak jest to pokazane na rysunku 2. Wykres ten różni się od wykresów funkcji, do jakich przyzwyczajono nas na lekcjach matematyki tym, że oś argumentów (czyli oś czasu $t$) jest ustawiona pionowo, a nie poziomo oraz tym, że zbiór wartości tej funkcji jest trójwymiarowy i w związku z tym wymaga użycia trzech osi (są to osie współrzędnych $x,y$ i $z$). Tak skonstruowany wykres funkcji jest krzywą w czterowymiarowej czasoprzestrzeni zwaną linią świata danego ciała.

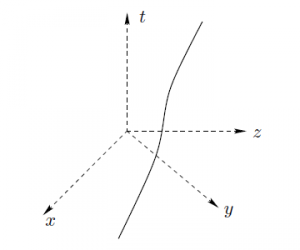Rysunek 2: Linia świata.

Istotną cechą czasoprzestrzeni jest to, że posiada ona swoją geometrię, która z kolei pozwala mówić o długości linii świata — ściśle mówiąc, taką długość potrafimy przyporządkować odcinkowi linii świata znajdującemu się pomiędzy wybranymi zdarzeniami (czyli punktami czasoprzestrzeni) leżącymi na tej linii.

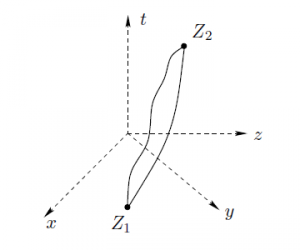Rysunek 3: Linie świata łączące ustalone zdarzenia $Z_1$ i $Z_2$.

Podobnie jak w przypadku długości krzywych w zwykłej trójwymiarowej przestrzeni, jeżeli dwa zdarzenia $Z_1$, $Z_2$ mogą być połączone różnymi liniami świata (rysunek 3) to linie te mogą mieć różną długość. Co więcej, można udowodnić, że spośród wszystkich linii świata łączących dwa ustalone punkty najdłuższą linią świata jest odcinek linii prostej łączącej te dwa punkty.

Mamy tu więc prawie pełną analogię pomiędzy własnościami długości krzywych w trójwymiarowej przestrzeni i własnościami długości linii świata ciał w czasoprzestrzeni — zastrzeżenie „prawie” odnosi się do tego, że odcinek linii prostej jest w zwykłej przestrzeni najkrótszą krzywą łączącą dwa ustalone punkty, a w czasoprzestrzeni (szczególnej teorii względności) jest najdłuższą linią świata łączącą parę wybranych punktów  (ta różnica może wydawać się zaskakująca, a być może nawet absurdalna, ale wynika ona w naturalny sposób stąd, że długość linii świata w czasoprzestrzeni jest obliczana w trochę inny sposób niż długość krzywej w przestrzeni — patrz dodatek matematyczny na dole niniejszej strony).

Opisana powyżej analogia pomiędzy własnościami geometrycznymi krzywych i linii świata może być użyta do prostego wyjaśnienia paradoksu bliźniąt.

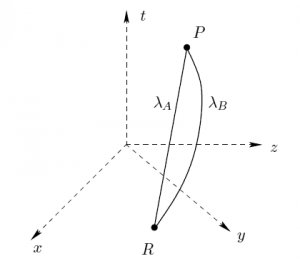Rysunek 4: Odcinki linii świata bliźniaków $A$ i $B$ pomiędzy zdarzeniami $R$ i $P$.

Rozważmy zatem dwóch bliźniaków, nazywając jednego z nich bliźniakiem $A$, a drugiego bliźniakiem $B$. Przyjmijmy, że bliźniak $A$ jest obserwatorem inercjalnym, zaś bliźniak $B$ w pewnym momencie $R$ (od ”rozstania się”) opuszcza swego brata wyruszając w długą podróż i powraca do niego w przyszłości w momencie $P$ (od „powrotu”). Zauważmy teraz, że zdarzenia $R$ i $P$ są punktami należącymi zarówno do linii świata bliźniaka $A$ jak i do linii świata bliźniaka $B$. Oznaczmy odcinek linii świata bliźniaka $A$ wyznaczony przez zdarzenia $R$ i $P$ symbolem $\lambda_A$, a analogiczny odcinek linii świata bliźniaka $B$ symbolem $\lambda_B$ tak jak to jest pokazane na rysunku 4. Oznaczmy ponadto czasoprzestrzenne długości odcinków $\lambda_A$ i $\lambda_B$ symbolami, odpowiednio, $d_A$ i $d_B$. Z geometrycznego punktu widzenia odcinki $\lambda_A$ i $\lambda_B$ są różnymi czasoprzestrzennymi krzywymi łączącymi ustalone punkty $R$ i $P$. Nie powinno być więc dla nas żadnym zaskoczeniem, gdyby okazało się, że ich długości $d_A$ i $d_B$ nie są sobie równe.

I tak jest w rzeczywistości. Otóż linia świata każdego obserwatora inercjalnego jest linią prostą. Skoro założyliśmy, że bliźniak $A$ jest takim obserwatorem to krzywa $\lambda_A$ jest odcinkiem linii prostej i w konsekwencji jest najdłuższą linią świata łączącą zdarzenia $R$ i $P$. Wynika stąd od razu, że długość każdego innego odcinka linii świata łączącego $R$ i $P$ musi być mniejsza od długości $d_A$. W szczególności zachodzi to dla odcinka $\lambda_B$ linii świata bliźniaka $B$:

\[
d_A>d_B.
\]

Aby doprowadzić do końca wyjaśnienie paradoksu bliźniąt trzeba jeszcze odwołać się do dwóch faktów związanych z fizyczną interpretacją czasoprzestrzennych wielkości geometrycznych.

Po pierwsze, długość odcinka linii świata danego ciała pomiędzy zdarzeniami $Z_1$ i $Z_2$ to upływ czasu jaki pomiędzy tymi zdarzeniami odmierzy zegar przytwierdzony do tego ciała i poruszający się wraz z nim. Zatem $d_A$ to czas, jaki z punktu widzenia bliźniaka $A$ upłynie od rozstania się $R$ z bratem do jego powrotu $P$, zaś $d_B$ to czas jaki pomiędzy tymi dwoma zdarzeniami upłynie z punktu widzenia bliźniaka $B$. Ponieważ $d_A>d_B$, więc w chwili $P$ bliźniak $B$ będzie młodszy od bliźniaka $A$.

Po drugie, linia świata będąca linią prostą opisuje ruch bez przyspieszenia, a przyspieszenie ciała objawia się tym, że jego linia świata odchyla się od linii prostej. A zatem wolniejsze starzenie się bliźniaka $B$ w porównaniu ze starzeniem się bliźniaka $A$ rzeczywiście jest związane z faktem, że bliźniak $B$ doznaje przyspieszenia na pewnych etapach swojej podróży, podczas gdy bliźniak $A$ porusza się ruchem nieprzyspieszonym.

Warto jeszcze dodać, że dla zaistnienia owej różnicy w starzeniu się bliźniaków nie jest konieczne, aby bliźniak $B$ poruszał się w stosunku do swojego brata z prędkością bliską prędkości światła — efekt ten zachodzi przy dowolnych (niezerowych) wartościach tej prędkości, przy czym oczywiście dla prędkości znacznie mniejszych od prędkości światła będzie on w praktyce niezauważalny.

Dlaczego  czas w poruszającym się  obiekcie płynie inaczej?

Zacznijmy od uściślenia stwierdzenia mówiącego, że „czas w poruszającym się obiekcie płynie inaczej”. Poprawne sformułowanie tego stwierdzenia brzmi: jeżeli dwóch obserwatorów poruszających się względem siebie obserwuje te same zdarzenia $Z$ oraz $Z’$ i za pomocą swoich zegarów mierzy upływ czasu pomiędzy tymi zdarzeniami to w większości przypadków otrzymają oni inny wynik.

Dlaczego tak jest? Na to pytanie można próbować odpowiedzieć odwołując się do niezależności prędkości światła od obserwatora inercjalnego.

Otóż załóżmy, że dwaj tacy obserwatorzy ${\cal O}_1$ i ${\cal O}_2$ poruszają się względem siebie i rozważmy dwa zdarzenia $Z$ i $Z’$, które z punktu widzenia obserwatora ${\cal O}_1$  zachodzą w tym samym miejscu. Na przykład, obserwator ${\cal O}_1$ posiada pewne urządzenie, które spoczywa względem niego i zdarzenie $Z$ to włączenie tego urządzenia, a $Z’$ to wyłączenie tego urządzenia. Z punktu widzenia obserwatora ${\cal O}_1$ odległość $\Delta d_1$ pomiędzy tymi zdarzeniami jest równa zeru. Ale ponieważ to urządzenie porusza się względem obserwatora ${\cal O}_2$ więc z jego punktu widzenia zdarzenia $Z$ i $Z’$ zachodzą w różnych miejscach i odległość $\Delta d_2$ między nimi jest różna od zera.

Z tego krótkiego rozumowania płynie wniosek, że różni obserwatorzy zmierzą w ogólności różne odległości pomiędzy ustalonymi zdarzeniami $Z,Z’$.

Wyobraźmy sobie teraz układ złożony z oddalonych od siebie źródła i detektora światła. Niech zdarzenie $Z$ będzie teraz emisją błysku światła przez źródło, a zdarzenie $Z’$ zarejestrowaniem tego błysku przez detektor. Znając względne prędkości obserwatorów ${\cal O}_1$ i ${\cal O}_2$ zawsze możemy w taki sposób ustawić źródło i detektor, że odległość $\Delta d_1$ pomiędzy $Z$ i $Z’$ mierzona przez ${\cal O}_1$ będzie inna niż odległość $\Delta d_2$ pomiędzy tymi zdarzeniami mierzona przez ${\cal O}_2$:

\[
\Delta d_1\neq \Delta d_2.
\]

Oznaczmy z kolei przez $\Delta t_1$ upływ czasu pomiędzy zdarzeniami $Z$ i $Z’$ mierzony przez obserwatora ${\cal O}_1$, a symbolem $\Delta t_2$ upływ czasu pomiędzy tymi zdarzeniami  mierzony przez obserwatora ${\cal O}_2$.

Zauważmy, że z punktu wiedzenia obserwatora ${\cal O}_1$ błysk światła poruszając się pomiędzy źródłem a detektorem przebył drogę $\Delta d_1$ w czasie $\Delta t_1$, zaś z punktu widzenia obserwatora ${\cal O}_2$ ten sam błysk przebył drogę $\Delta d_2$ w czasie $\Delta t_2$, co pozwala nam łatwo obliczyć wartość prędkości światła względem jednego i drugiego obserwatora. Ale wartość tej prędkości jest taka sama dla obu obserwatorów:

\[
\frac{\Delta d_1}{\Delta t_1}=\frac{\Delta d_2}{\Delta t_2}.
\]

Biorąc pod uwagę, że odległość $\Delta d_1$ nie jest równa odległości $\Delta d_2$ dochodzimy do wniosku, że

\[
\Delta t_1\neq \Delta t_2.
\]

Powyższe rozumowanie pokazuje, że jeżeli wartość prędkości światła jest taka sama dla wszystkich obserwatorów inercjalnych, to upływ czasu pomiędzy parą zdarzeń $Z,Z’$ będzie różny dla różnych obserwatorów.

Dodatek matematyczny

Niech krzywa $\gamma$ będzie krzywą w trójwymiarowej przestrzeni łączącą dwa ustalone punkty $a$ i $b$. Wyobraźmy sobie ciało poruszające się wzdłuż tej krzywej w ten sposób, że w chwili $t_1$ rozpoczyna ono ruch z punktu $a$, a do punktu $b$ dociera w chwili $t_2$. Jeżeli prędkość tego ciała zmienia się w czasie jak $\vec{v}(t)$, to długość $d_\gamma$ krzywej $\gamma$ można obliczyć ze wzoru

\[
d_\gamma=\int_{t_1}^{t_2} \sqrt{\vec{v}(t)\cdot\vec{v}(t)}\,dt,
\]

gdzie $\vec{u}\cdot\vec{w}$ oznacza iloczyn skalarny wektorów $\vec{u}$ i $\vec{w}$.

Jeżeli $\lambda$ jest odcinkiem linii świata pewnego ciała łączącym dwa zdarzenia $Z_1$ i $Z_2$, to długość $d_\lambda$ tego odcinka zdefiniowana jest w następujący sposób:

\[
d_\lambda=\frac{1}{c}\int_{t_1}^{t_2} \sqrt{c^2-\vec{v}(t)\cdot\vec{v}(t)}\,dt
\]

— $t$ jest tutaj czasem mierzonym przez dowolnie wybranego obserwatora inercjalnego, $t_1$ i $t_2$ są chwilami, w których (z punktu widzenia tego obserwatora) zachodzą zdarzenia $Z_1$ i $Z_2$, $\vec{v}(t)$ jest prędkością ciała względem owego obserwatora, a $c$ jak zawsze wartością prędkości światła w próżni.