Wiemy z codziennego doświadczenia, że większość ciał ulega rozszerzaniu przy wzroście ich temperatury. Na poziomie makroskopowym liniowy wzrost długości $\Delta L$ przy wzroście temperatury o $\Delta T$ opisuje prawo

$$
\Delta L= \alpha L \Delta T,
$$

gdzie $L$ jest długością początkową, a $\alpha$ jest współczynnikiem rozszerzalności liniowej. To prawo jest słuszne dla małych $\Delta T$. Analogicznie, objętość ciała zmienia się o $\Delta V$ zgodnie z równaniem

$$
\Delta V= \beta V \Delta T,
$$

gdzie $V$ jest objętością początkową, a $\beta$ jest współczynnikiem rozszerzalności objętościowej. W przybliżeniu zachodzi $\beta \approx  3 \alpha$.

Ciało rozszerza się we wszyskich kierunkach. Płytka o przekroju kwadratowym (ciągła  niebieska linia) zwiększy swoje pole (przerywana  czerwona linia) co ilustruje rys. a. Jeśli narysujemy na środku koło (linią na niebiesko), to po wzroście temperatury koło to rozszerzy się do czerwonej linii przerywanej, rys. a.

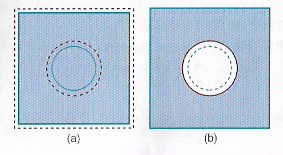
Jeśli zamiast rysowania koła wytniemy okrągłą dziurę, jak na rys. b zaznaczono przerywaną niebieską linią, to przy wzroście temperatury reszta płytki rozszerza się tak samo jak poprzednio, czyli pole koła wzrasta i jest zaznaczone linią czerwoną ciągłą.

Dla grubościennej rury oczekujemy podobnego efektu, promień zewnętrzny i promień wewnętrzny się zwiększa w trakcie podgrzewania. Oczywiście w trzecim kierunku rura się wydłuża.

Opisany efekt rozszerzania się pola przekroju wewnętrznego wydrążenia znajduje zastosowanie w przemyśle. Chcąc osadzić metalowy trzpień lub nit w otworze innego kawałka metalu należy ten metal rozgrzać, umieścić w nim dopasowany nit i całość ochłodzić.