Zadane tu pytanie dotyczy tak naprawdę jednego z trudniejszych problemów, z jakimi mamy do czynienia w ogólnej teorii względności (OTW), a mianowicie problemu odróżniania pozornych osobliwości pola grawitacyjnego od jego prawdziwych osobliwości. Dlatego też odpowiedź na to pytanie będzie dość długa. Będzie się ona składać z dwóch części — pierwsza część będzie dotyczyła zachowania się obiektów punktowych, zaś druga obiektów rozciągłych. Dla uproszczenia wzorów będziemy stosować jednostki geometryczne, w których stała grawitacyjna $G$ i wartość prędkości światła w próżni $c$ mają wartość 1.

Obiekty punktowe

W wielu sytuacjach w fizyce wygodnie jest zaniedbać rozciągłość danego ciała i traktować je jako obiekt punktowy — każdy taki obiekt będziemy nazywać cząstką.

Równanie ruchu cząstki próbnej

W ogólnej teorii względności (OTW) ruch każdej cząstki próbnej jest opisany za pomocą linii świata. Linia świata danej cząstki musi spełniać pewne równanie ruchu będące uogólnieniem II zasady dynamiki Newtona. Przypomnijmy, że zasada ta głosi, że przyspieszenie czyli zmiana prędkości $\vec{v}$ ciała w czasie $t$ pomnożone przez masę ciała jest równe działającej na to ciało sile $\vec{F}$:
\begin{equation}
m\frac{d\vec{v}}{dt}=\vec{F}.
\label{II-newt}
\end{equation}
Powyższe równanie uogólnia się w OTW na przypadek cząstki o niezerowej masie w następujący sposób.

Danej cząstce o masie $m\neq 0$ przypisujemy czteroprędkość $U$, która jest wektorem o jednostkowej długości stycznym do jej linii świata, a następnie żądamy, aby zmiana czteroprędkości cząstki wzdłuż linii świata pomnożona przez masę $m$ była równa sile $F$ działającej na cząstkę. Przełożenie tej zasady na język matematyki napotyka jednak pewną trudność: opisanie zmiany czteroprędkości wzdłuż linii świata wymaga porównywania wektorów stycznych do tej linii w różnych jej punktach, a w przestrzeniach, których używa się w OTW do modelowania czasoprzestrzeni nie istnieje naturalny sposób na porównywanie wektorów związanych z różnymi punktami takiej przestrzeni. W konsekwencji do opisania zmiany czteroprędkości nie można użyć zwykłej pochodnej takiej jak pochodna $d/dt$ użyta w równaniu \eqref{II-newt}. Zamiast niej stosuje się tzw. pochodną kowariantną $\nabla$, do konstrukcji której używa się wielkości opisujących pole grawitacyjne istniejące w danej czasoprzestrzeni. Tak więc w OTW to pochodna kowariantna $\nabla U$ czteroprędkości opisuje jej zmianę wzdłuż linii świata cząstki co oznacza, że $\nabla U$ jest odpowiednikiem przyspieszenia cząstki. Wobec tego w OTW równanie ruchu cząstki w przybiera postać
\begin{equation}
m\nabla U=F,
\label{nab}
\end{equation}
gdzie $F$ jest czterowektorem siły działającej na cząstkę. Należy tu podkreślić, że $F$ opisuje wpływ na cząstkę wszystkich pól i ciał za wyjatkiem pola grawitacyjnego ponieważ wpływ tego ostatniego jest już uwzględniony w konstrukcji pochodnej $\nabla$.

Jeżeli na cząstkę nie działają żadne niegrawitacyjne siły (lub jeśli ich działanie się znosi) to $F=0$ i równanie ruchu takiej cząstki przyjmuje postać
\begin{equation}
\nabla U=0
\label{geo}
\end{equation}
— cząstkę taką nazywamy swobodną i mówimy o niej, że porusza się (lub też spada) swobodnie w polu grawitacyjnym. Linię świata cząstki swobodnej, a więc linię spełniającą równanie \eqref{geo} nazywamy krzywą geodezyjną lub po prostu geodezyjną — z geometrycznego punktu widzenia geodezyjna jest uogólnieniem linii prostej na przypadek zakrzywionej przestrzeni. Z porównania równań \eqref{nab} i \eqref{geo} widać, że pochodną $\nabla U$ możemy potraktować jako miarę tego, jak bardzo linia świata danej cząstki odbiega od krzywej geodezyjnej.

Siły działające na cząstkę w jej układzie odniesienia

Ustalmy teraz cząstkę próbną i rozważmy układ odniesienia, w którym dana cząstka spoczywa — taki układ będziemy tu nazywać układem cząstki. Skoro cząstka spoczywa względem tego układu to w tym układzie powinna na nią działać pewna dodatkowa siła $\bar{F}$ równoważąca działanie siły $F$ czyli siła o tym samym kierunku, tej samej wartości lecz zwrocie przeciwnym do siły $F$:
\[
\bar{F}=-F.
\]
I tak jest w rzeczywistości — jeżeli równanie \eqref{nab} przedstawimy za pomocą współrzędnych związanych z układem cząstki to z pochodnej $\nabla U$ w naturalny sposób wyodrębnia się pewien wyraz, który (po pomnożeniu przez masę $m$) pełni rolę siły $\bar{F}$.

Czym jest siła $\bar{F}$? Skoro (formalnie rzecz biorąc) pochodzi ona z pochodnej $\nabla$, do określenia której użyto wielkości opisujących pole grawitacyjne to może jest to siła grawitacji działająca na cząstkę w jej układzie odniesienia? Ale zauważmy, że $\bar{F}$ jest niezerowa wtedy i tylko wtedy, gdy niezerowa jest siła $F$. A skądinąd wiadomo, że w układzie cząstki poruszającej się pod wpływem (niezerowej) siły pojawiają się siły bezwładności. Może więc $\bar{F}$ jest siłą bezwładności?

Co na ten temat mówi OTW? W istocie nic — OTW nie udziela odpowiedzi na pytanie czy $\bar{F}$ jest siłą grawitacji czy siłą bezwładności, pozwalając nam tym samym na pewną swobodę interpretacji.

Rozważmy dla przykładu osobę siedzącą w krzesełku obracającej się karuzeli. Na tę osobę działają dwie niegrawitacyjne siły: pionowa siła $F_1$ wywierana przez siedzenie krzesełka jest skierowana ku górze, a pozioma siła dośrodkowa $F_2$ wywierana przez oparcie krzesełka jest skierowana ku osi obrotu karuzeli. W tym przypadku siła $F=F_1+F_2$ jest niezerowa i linia świata tej osoby nie jest linią geodezyjną. W układzie tej osoby działają na nią dwie dodatkowe siły: $\bar{F}_1=-F_1$ i $\bar{F}_2=-F_2$. Siłę $\bar{F}_1$ w naturalny sposób interpretujemy jako siłę grawitacji, a siłę $\bar{F}_2$ jako siłę bezwładności (siłę odśrodkową). Zatem w tym przypadku siła $\bar{F}$ daje się przedstawić jako suma sił $\bar{F}_1$ i $\bar{F}_2$ o prostej i naturalnej interpretacji.

Rozważmy teraz kosmonautę poruszającego się na okołoziemskiej orbicie wyłacznie pod wpływem grawitacji. W tej sytuacji $F=0$, linia swiata kosmonauty jest geodezyjną i w konsekwencji w jego układzie odniesienia siła $\bar{F}=0$, co objawia się jako stan nieważkości.

Podsumowując powyższą część odpowiedzi podkreślmy, że w OTW w układzie odniesienia cząstki, na którą działa niezerowa niegrawitacyjna siła $F$ pojawia się siła $\bar{F}=-F$ i związane z nią przyspieszenie
\begin{equation}
\bar{a}=\frac{\bar{F}}{m}=-\nabla U
\label{acc}
\end{equation}
Siła ta i to przyspieszenie znikają natychmiast, gdy tylko pozwolimy cząstce poruszać się swobodnie w polu grawitacyjnym.

Przyspieszenie grawitacyjne na horyzoncie czarnej dziury Schwarzschilda

Czasoprzestrzeń na zewnątrz horyzontu czarnej dziury Schwarzschilda o masie $M$ jest statyczna, co w szczególności oznacza, że możemy stwierdzić czy dana masywna cząstka spoczywa względem czarnej dziury czy też nie. Rozważmy teraz cząstkę spoczywającą względem czarnej dziury, którą to cząstkę będziemy nazywać statyczną. Okazuje się, że linia świata każdej cząstki statycznej charakteryzuje się stałą wartością Schwarzschildowskiej współrzędnej radialnej $r$ tzn. cząstka taka spoczywa w punkcie o ustalonej współrzędnej $r$. Dodajmy tu, że współrzędna $r$ wchodzi w skład standardowego układu współrzędnych na czasoprzestrzeni Schwarzschilda — na zewnątrz czarnej dziury współrzędna ta przyjmuje wartości większe od $2M$, a granica $r\to 2M$ odpowiada zbliżaniu się do horyzontu czarnej dziury.

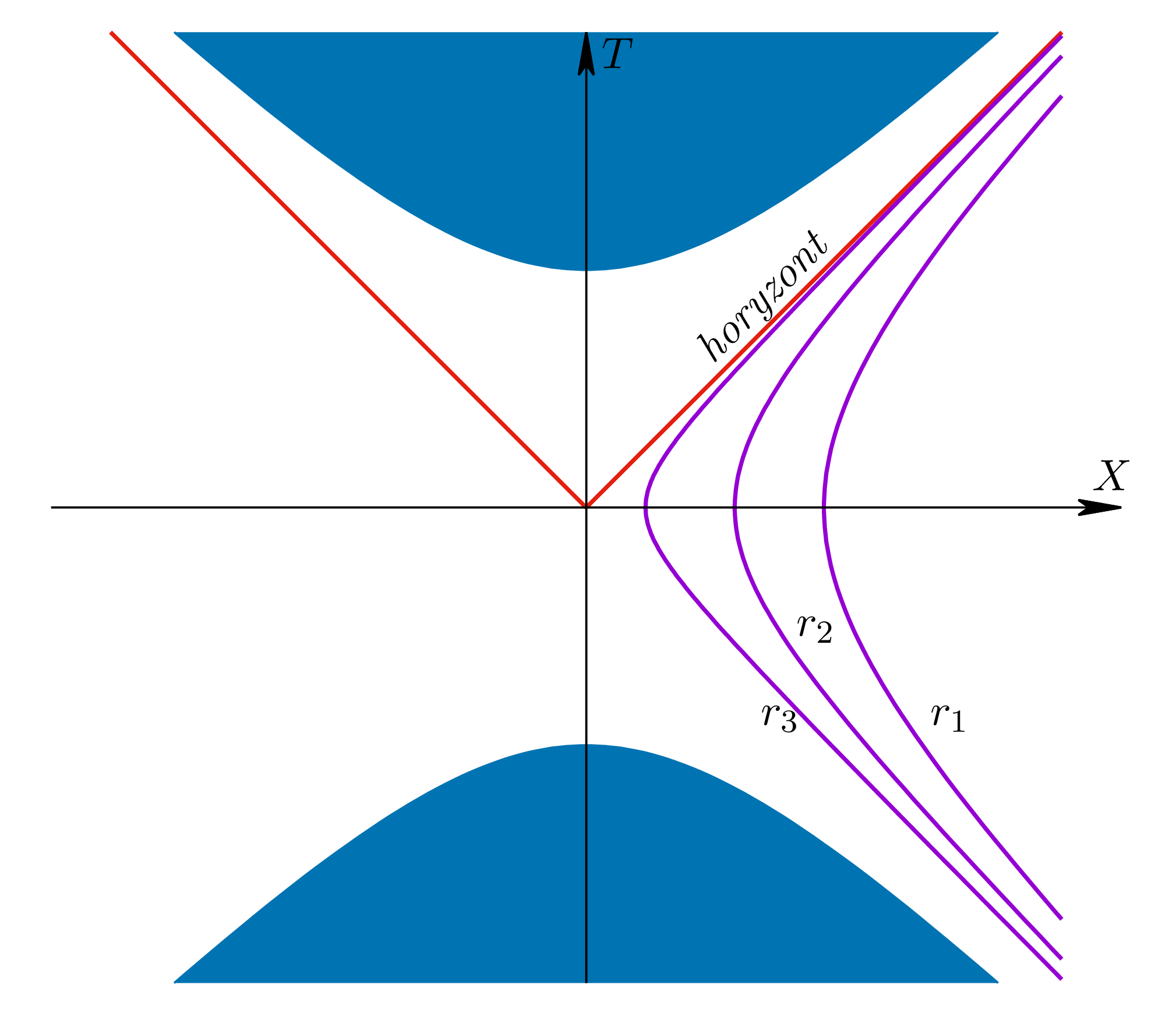
Rysunek 1

Rysunek 1 przedstawia czarną dziurę Schwarzschilda opisaną w tzw. współrzędnych Kruskala-Szekeresa. Czasoprzestrzeń na tym rysunku to biały obszar, horyzont czarnej dziury to czerwona linia składająca się z dwóch półprostych, dla których $r=2M$, a wnętrze czarnej dziury to obszar powyżej czerwonej linii. Trzy fioletowe hiperbole po prawej stronie rysunku to linie świata cząstek statycznych, dla których współrzędna radialna przyjmuje wartości, odpowiednio, $r_1>r_2>r_3>2M$ — im współrzędna radialna danej linii świata bliższa jest wartości $2M$ tym bliżej horyzontu czarnej dziury ta linia przebiega.

Obliczając wielkość $m\nabla U$ dla cząstki spoczywającej względem czarnej dziury w punkcie o współrzędnej $r$ otrzymujemy siłę $F$ jaka musi działać na tę cząstkę, aby utrzymać ją w niezmiennym położeniu względem czarnej dziury — siła ta jest oczywiście skierowana od czarnej dziury. Zatem w układzie tej cząstki pojawia się siła $\bar{F}$ skierowana ku czarnej dziurze o tej samej wartości co siła $F$. Ponieważ mamy tu doczynienia z cząstką spoczywającą względem czarnej dziury (czyli względem obiektu wytwarzającego pole grawitacyjne w czasoprzestrzeni) wydaje się rozsądnym zinterpretowanie siły $\bar{F}$ jako siły grawitacji działającej na tę cząstkę, a przyspieszenia \eqref{acc} jako przyspieszenia grawitacyjnego. Wartość tego przyspieszenia dla cząstki statycznej spoczywającej w punkcie o współrzędnej radialnej $r$ wynosi
\begin{equation}
|\bar{a}(r)|=\frac{M}{r^2}\frac{1}{\sqrt{1-2M/r}}.
\label{g}
\end{equation}

Tak jak to zauważono w pytaniu gdy $r\to 2M$ to wartość obliczonego powyżej przyspieszenia grawitacyjnego rośnie nieograniczenie:
\begin{equation}
\lim_{r\to 2M} |\bar{a}(r)|=\infty.
\label{nabU-r}
\end{equation}
A skoro dążenie $r\to 2M$ oznacza nieograniczone zbliżanie się do horyzontu czarnej dziury, to czy na podstawie powyższego wyniku możemy wnioskować o tym, że na horyzoncie czarnej dziury przyspieszenie grawitacyjne osiąga wartość nieskończoną? I czy wobec tego każda cząstka próbująca przekroczyć horyzont będzie doznawać na nim „nieskończonego” przyspieszenia lub też będzie poddawana działaniu sił o „nieskończonej wartości”?

Kontrprzykład

Rozważmy czasoprzestrzeń Minkowskiego wraz z układem współrzędnych $(t,x,y,z)$ pewnego obserwatora inercjalnego. W tej czasoprzestrzeni wyróżnimy stożek świetlny $S$ utworzony przez linie świata fotonów wyemitowanych we wszystkich kierunkach z punktu o współrzędnych $x=y=z=0$ w chwili $t=0$ i linię świata pewnej masywnej cząstki przecinającą ten stożek w punkcie $p$. Sytuacja ta zobrazowana jest na rysunku 2 — dwie czerwone półproste oznaczają stożek świetlny (ściślej: są przecięciem stożka z płaszczyzną $y=z=0$), a fioletowa krzywa jest linią świata cząstki.

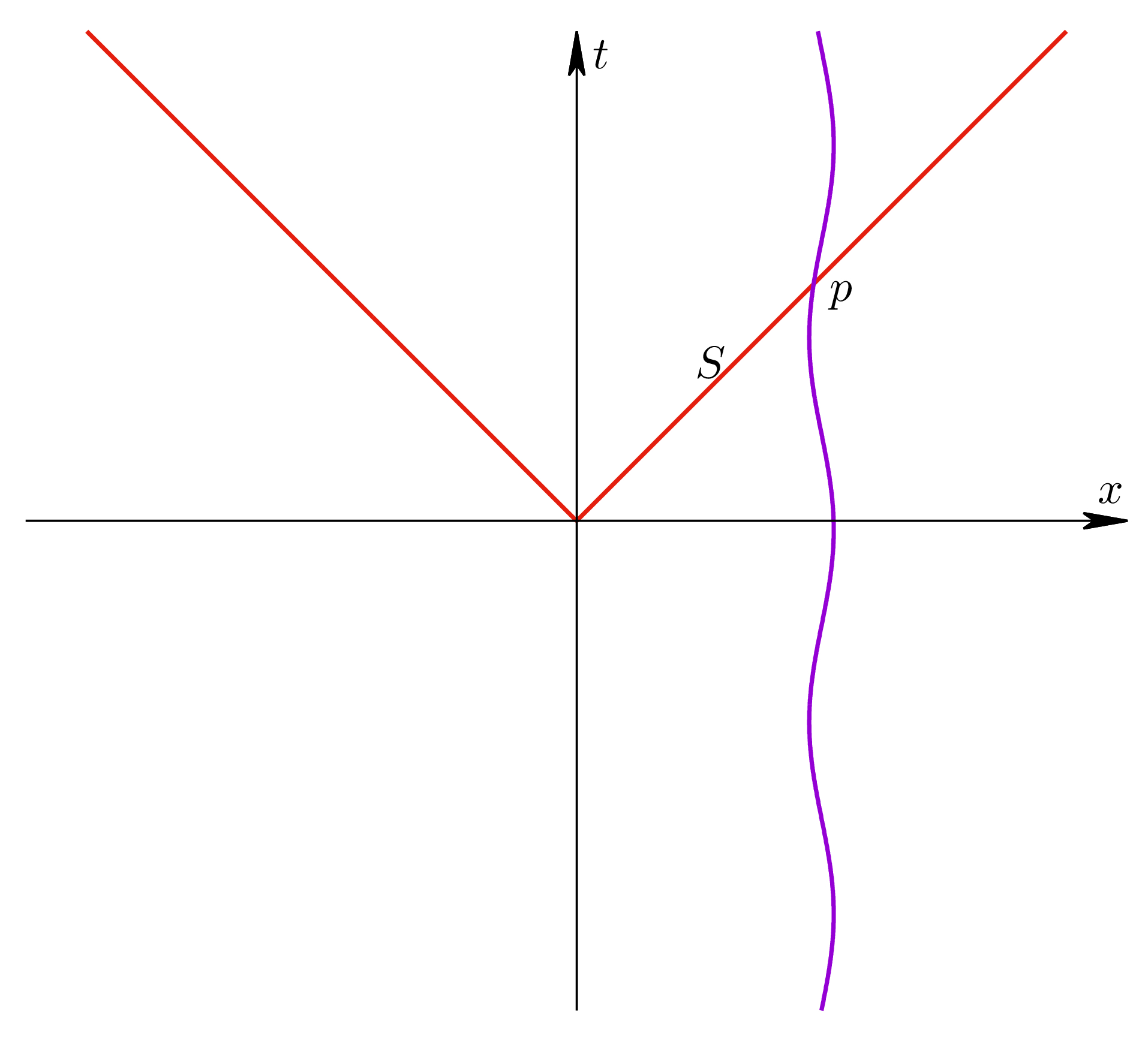
Rysunek 2

Jakie jest przyspieszenie $\bar{a}$, którego w swoim układzie doznaje cząstka na skutek działania siły $\bar{F}$ w punkcie $p$? Może ono być zupełnie dowolne np. równe zeru i zależy tylko tego, jaka niegrawitacyjna siła $F$ działa na cząstkę w punkcie $p$, natomiast fakt, że w punkcie $p$ linia świata cząstki przecina stożek $S$ nie ma tu żadnego znaczenia.

Rozważmy teraz rodzinę masywnych cząstek parametryzowaną zmienną $\lambda>0$, których linie świata zdefiniowane są w układzie współrzędnych $(t,x,y,z)$ jak następuje:
\begin{equation}
\tau\mapsto(\lambda\sinh(\tau/\lambda),\lambda\cosh(\tau/\lambda),0,0)
\label{ll}
\end{equation}
($\tau$ jest tu tzw. czasem własnym cząstki). Jak łatwo zauważyć, każda taka linia świata jest hiperbolą, a wraz ze zbliżaniem się parametru $\lambda$ do zera linie świata zbliżają się nieograniczenie do stożka $S$, co pokazano na rysunku 3, gdzie $\lambda_1>\lambda_2>\lambda_3>0$.

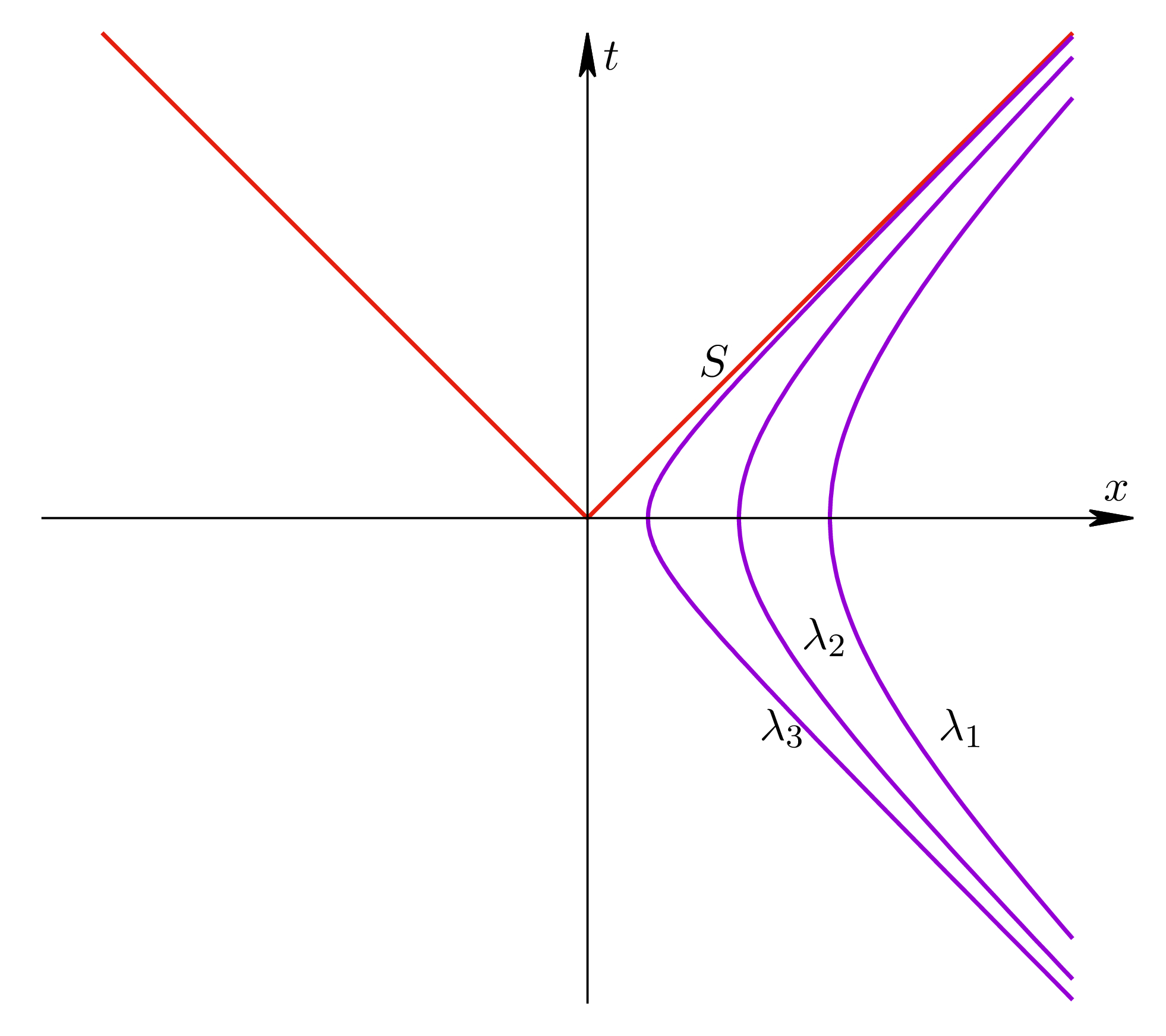
Rysunek 3

Przyspieszenie $\bar{a}(\lambda)$, jakiego w swoim układzie doznaje cząstka o linii świata zadanej parametrem $\lambda$, ma następującą wartość
\[
|\bar{a}(\lambda)|=\frac{1}{\lambda}
\]
skąd mamy
\[
\lim_{\lambda\to 0}|\bar{a}(\lambda)|=\infty
\]
A skoro dążenie $\lambda\to 0$ oznacza nieograniczone zbliżanie się do stożka $S$, to czy na podstawie powyższego wyniku możemy wnioskować o tym, że każda cząstka próbująca przekroczyć stożek będzie doznawać na nim „nieskończonego” przyspieszenia lub też będzie poddawana działaniu sił o „nieskończonej wartości”?

Odpowiedź na to pytanie została już udzielona wcześniej i brzmi: nie, na stożku $S$ nic takiego nie ma miejsca.

Analiza

Zauważmy następujące cechy wspólne obydwu sytuacji tzn. tej z czasoprzestrzeni Schwarzschilda i tej z czasoprzestrzeni Minkowskiego:

• w każdym przypadku mamy do czynienia z rodziną linii świata cząstek masywnych: w pierwszym przypadku jest to rodzina linii świata cząstek statycznych, która parametryzowana jest współrzędną radialną $r>2M$, w drugim jest to rodzina linii świata \eqref{ll} parametryzowana zmienną $\lambda>0$.
• w granicy $r\to 2M$ linie świata cząstek statycznych zbliżają się nieograniczenie do horyzontu czarnej dziury, ale żadna z nich horyzontu nie przecina; w granicy $\lambda\to 0$ linie świata \eqref{ll} zbliżają się nieograniczenie do stożka $S$, ale żadna z nich stożka nie przecina.
• w granicy $r\to 2M$ wartość przyspieszenia $\bar{a}(r)$ istniejącego w układzie danej cząstki statycznej rośnie nieograniczenie; w granicy $\lambda\to 0$ wartość przyspieszenia $\bar{a}(\lambda)$ istniejącego w układzie danej cząstki o linii świata \eqref{ll} rośnie nieograniczenie.

W przypadku czasoprzestrzeni Minkowskiego istnienie takiej rodziny linii świata nie oznacza jednak, że każda cząstka przekraczająca stożek $S$ będzie doznawała na nim „nieskończonego przyspieszenia”. Widać więc, że nie można automatycznie przenosić wartości przyspieszeń $\bar{a}(\lambda)$ obliczonych w sąsiedztwie stożka na sam stożek. A nie można z następującego powodu: przyspieszenie $\bar{a}(\lambda)$ nie jest cechą punktu czasoprzestrzeni, przez który przechodzi linia świata \eqref{ll} ani pola grawitacyjnego w tym punkcie, lecz cechą tej linii świata — wynika to wprost ze wzoru \eqref{acc} — i w konsekwencji przez ten sam punkt można przeprowadzić inną linię świata o dowolnie wybranym przyspieszeniu $\bar{a}$. Tak więc punktom $(p_n)$ tworzącym ciąg zbiegający do punktu $p$ leżącego na stożku $S$ można przyporządkować przyspieszenia o dowolnej wartości $|\bar{a}(p_n)|$, a tak utworzony ciąg wartości może dążyć do dowolnej skończonej bądź nieskończonej granicy wraz ze zbliżaniem się punktów $(p_n)$ do punktu $p$.

Zatem ze względu na ogromną dowolność w konstruowaniu tego typu ciągów w sąsiedztwie stożka $S$ nie można na podstawie granic tych ciągów wnioskować o tym, co dzieje się na samym stożku.

Skąd więc wiemy, że na stożku $S$ nie dzieje się nic osobliwego? Stąd, że potrafimy znaleźć układ odniesienia, który jest zdefiniowany nie tylko w sąsiedztwie stożka (tak jak linie świata \eqref{ll}), ale również i na samym stożku i w którym to układzie wszystkie wielkości opisujące pole grawitacyjne przyjmują skończone wartości — tu takim układem jest np. użyty powyżej układ współrzędnych $(t,x,y,z)$.

Czy więc każda cząstka przekraczająca horyzont czarnej dziury Schwarzschilda będzie doznawać na nim „nieskończonego przyspieszenia”? Nie, jeżeli istnieje układ odniesienia zdefiniowany i na horyzoncie i w jego sąsiedztwie, w którym wszystkie wielkości opisujące pole grawitacyjne przyjmują skończone wartości. Okazuje się, że taki układ istnieje — jest to wspomniany powyżej układ Kruskala-Szekeresa. Z istnienia tego układu wynika, że przyspieszenie $\bar{a}$ jakiego w swoim układzie doznaje cząstka przekraczająca horyzont nie ma żadnego związku z przyśpieszeniami doznawanymi przez cząstki statyczne na zewnątrz horyzontu, lecz zależy tylko i wyłącznie od niegrawitacyjnej siły $F$ działającej w tym momencie na tą cząstkę — np. cząstka swobodna ($F=0$) przechodzi przez horyzont zupełnie „bezboleśnie”.

Obiekty rozciągłe

Naprężenia w ciele rozciągłym na horyzoncie supermasywnej czarnej dziury

Rozważmy teraz ciało rozciągłe umieszczone w polu grawitacyjnym zakładając, że nie działają na nie żadne zewnętrzne siły niegrawitacyjne. Okazuje się, że w takiej sytuacji pole grawitacyjne wywołuje w ciele naprężenia, które są proporcjonalne do tensora czasoprzestrzennej krzywizny obliczonego w punktach, w których w danym momencie to ciało się znajduje. Dla czarnej dziury Schwarzschilda wartość tensora krzywizny na horyzoncie jest rzędu $M^{-2}$, a szczegółowe rachunki wykorzystujące ten fakt pokazują, że dla supermasywnych czarnych dziur o masie dziesiątków milionów mas Słońca wartości tensora krzywizny na horyzoncie są porównywalne z wartościami tensora krzywizny w otoczeniu Ziemi. Dlatego w ciele rozciągłym przekraczającym horyzont takiej czarnej dziury pojawią się naprężenia podobne do tych jakich doświadcza ciało rozciągłe poruszające się swobodnie w polu grawitacyjnym Ziemi – takie naprężenia są bardzo małe i ciało rozciągłe pokona horyzont takiej czarnej dziury nie doświadczając niczego szczególnego.

Osobliwość w $r=0$

Okazuje się jednak, że w czasoprzestrzeni Schwarzschilda wartości tensora czasoprzestrzennej krzywizny dążą do nieskończoności gdy $r\to 0$. Oznacza to, że w każdym ciele rozciągłym, które przekroczyło horyzont czarnej dziury i zbliża się do punktu $r=0$ (a skądinąd wiadomo, że po przekroczeniu horyzontu to zbliżanie się jest nieuchronne) naprężenia wywołane przez pole grawitacyjne rosną nieograniczenie.

Skoro tensor krzywizny jest wielkością charakteryzującą pole grawitacyjne w czasoprzestrzeni to czy na podstawie powyższych faktów można twierdzić, że pole grawitacyjne osiąga w $r=0$ wartości nieskończone lub że pojawiają się tam nieskończone siły czy nieograniczone przyspieszenia grawitacyjne? W rzeczywistości lepiej jest odpowiedzieć na pytanie, czy istnieje układ odniesienia zdefiniowany i w punkcie $r=0$ i w jego sąsiedztwie, w którym wszystkie wielkości opisujące pole grawitacyjne przyjmują skończone wartości.

Okazuje się, że odpowiedź na to pytanie brzmi: nie, taki układ nie istnieje. I ten fakt jest podstawą do uznania punktu $r=0$ za osobliwość pola grawitacyjnego w czasoprzestrzeni Schwarzschilda.

Podsumowanie

W OTW dość często mamy do czynienia z sytuacją, w której pewne wielkości opisujące pole grawitacyjne dążą do nieskończonych wartości przy zbliżaniu się do pewnych punktów. Jednakże nie musi to oznaczać, że w tych punktach samo pole jest osobliwe, gdyż te wielkości dość często zależą nie tylko od pola grawitacyjnego, ale też od innych czynników — przykładem takiej wielkości jest omawiane powyżej przyspieszenie $\bar{a}$, które zależy od niegrawitacyjnej siły działającej na daną cząstkę i tylko w niektórych szczególnych sytuacjach (np. gdy cząstka jest statyczna) może być interpretowane jako wielkość opisująca pole grawitacyjne.

Dlatego też właściwym kryterium określającym, czy pole grawitacyjne w danym punkcie czasoprzestrzeni jest osobliwe czy nie, jest kryterium istnienia odpowiedniego układu odniesienia: jeżeli istnieje układ odniesienia określony w danym punkcie i w jego sąsiedztwie taki, że wszystkie wielkości opisujące pole grawitacyjne w tym układzie są skończone, to uznajemy, że w tym punkcie pole jest regularne — w przeciwnym przypadku pole w tym punkcie traktujemy jako osobliwe. W przypadku czasoprzestrzeni Schwarzschilda na mocy tego kryterium uznajemy, że na horyzoncie czarnej dziury ($r=2M$) pole grawitacyjne jest regularne (innymi słowy, osobliwość jest tu pozorna), natomiast w punkcie $r=0$ występuje (prawdziwa) osobliwość pola.