Wszystko się sprowadza do dokładności z jaką chcemy opisać daną sytuację. Wiadomo już, że teoria względności została potwierdzona doświadczalnie i stanowi ona lepszy model od mechaniki klasycznej. Czy to oznacza, że powiniśmy wyrzucić do kosza cały ten formalizm i zastąpić go nowym, który jest bardziej skomplikowany matematycznie, ale daje lepsze rezulaty? Zbadajmy na przykład zjawisko, które się pojawia w szczególnej teorii względności: skrócenie Lorentza. Polega ono na tym, że poruszający się w odniesieniu do nas obiekt będzie „skurczony”… ale ilukrotnie skurczony? Teoria względności ma na to odpowiedź w postaci czynnika Lorentza:

\[\gamma = \frac{1}{\sqrt{1 – \frac{v^{2}}{c^{2}}  }},\]

który określia ilukrotnie skrócony został dany obiekt (czyli np. gdyby $\gamma = 2$ to obiekt byłby dwa razy krótszy w porównaniu do jego spoczywającej wersji). Prędkość obiektu w powyższym wzorze $v$ możemy określić jako pewną część prędkości światła $c$ (na przykład $0,1 c$ oznaczałoby jedną dziesiątą prędkości światła). W celu lepszego zobarazowania jak prędkość obiektu wpływa na rozmiar z jakim go obserwujemy wykreślmy powyższą zależność:

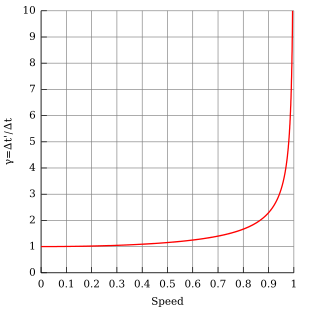
Na osi pionowej mamy informację o krotności skurczenia się danego obiektu, na osi poziomej prędkość się porusza się on względem prędkości światła. Widzimy, że krzywa „odrywa” się od jedności dopiero w okolicach $v = 0,4 c$. Dla prędkości $v = 0,01c$ czynnik Loretnza wynosi $1,0000500…$, więc do tej prędkości nie powinniśmy się za bardzo martwić o efekty relatywistyczne. Natomiast warto zwrócić uwagę, jak ogromna jest ta prędkość!
Jest to $10\, 800\, 000$ km/h, czyli około $77\, 142$ razy więcej, niż samochód pędzący z maksymalną dopuszczoną prędkością na autostradzie. I nawet przy tej prędkości nie musimy się za bardzo martwić o efekty relatywistyczne.

Polecam także taki filmik, który pokazuje jakby wyglądała rzeczywistość dla obserwatora poruszającego się z prędkością $0,8c$.