Przyciąganie elektronu i protonu można wyjaśnić na poziomie kwantowej teorii pola. Nośnikiem oddziaływania elektromagnetycznego między protonem i elektronem jest foton. Okazuje się, że jeśli nośnikiem oddziaływania jest cząstka o spinie 1, jak jest w przypadku fotonu, to cząstki obdarzone ładunkiem o przeciwnym znaku przyciągają się. Gdyby nośnikiem oddziaływania była cząstka o spinie 0 lub 2, to ładunki o przeciwnym znaku odpychałyby się.  

Fakt, że proton i elektron mogą tworzyć stan związany, czyli atom wodoru, wynika z fundamentalnej własności mechaniki kwantowej, według której z elektronem związana jest fala prawdopodobieństwa określająca prawdopodobieństwo znalezienia elektronu w danym miejscu. Zgodnie z intuicją fizyki klasycznej, środek jądra to punkt, w którym istnieje największe prawdopodobieństwo znalezienia elektronu. Jednakże niezerowe prawdopodobieństwo znalezienia elektronu jest również w innych punktach przestrzeni, w wyniku czego średnia wartość odległości elektronu od jądra jest różna od zera.

Równania kwantowej teorii pola, w szczególności elektrodynamiki kwantowej, są na tyle skomplikowane, że nie można ich dokładnie rozwiązać nawet w tak prostym przypadku jak oddziaływanie elektromagnetyczne protonu i elektronu. W związku z tym stosuje się przybliżoną metodę rozwiązywania tych równań zwaną rachunkiem perturbacyjnym. Graficznym przedstawieniem tej metody są diagramy Feynmanna. Każdy diagram Feynmanna opisuje pewien wkład do końcowego rozwiązania. Rachunek perturbacyjny oparty na diagramach Feynmanna może być z powodzeniem stosowany, jeśli możliwe jest wyodrębnienie i policzenie diagramów Feynmanna, które mają dominujący wkład do końcowego wyniku. Ta metoda sprawdza się bardzo dobrze w opisie rozpraszania elektronów i protonów, gdyż w pierwszym przybliżeniu można opisać to oddziaływanie jako wymianę pojedynczego fotonu, które jest stosunkowo dobrym przybliżeniem. Ponadto wynik ten można jeszcze udoskonalić licząc tzw. poprawki pętlowe (diagramy Feynmanna, w których linie reprezentujące cząstki tworzą pętle), przy czym te poprawki dają do końcowego wyniku mniejszy wkład niż wymiana pojedynczego fotonu.

Opis stanów związanych, takich jak na przykład atom wodoru, jest dużo bardziej skomplikowany, gdyż nie można używać standardowego rachunku perturbacyjnego kwantowej teorii pola (dlatego często nazywa się takie układy nieperturbacyjnymi). W języku diagramów Feynmanna takie stany opisywane byłyby przez wymianę między elektronem i protonem nieskończonej liczby fotonów tworzących nieskończonie dużo pętli.

Mimo wszystko, w przypadku atomu wodoru możliwe jest bardzo dokładne policzenie jego własności, w tym położenia poziomów energetycznych elektronu. Wynika to z tego, że w dobrym przybliżeniu atom wodoru można opisać w sposób nierelatywistyczny. Równaniem ruchu w nierelatywistycznej mechanice kwantowej jest równanie Schroedingera, które dla potencjału Coulomba (będący dominującym efektem wiążącym elektron z protonem) można rozwiązać dokładnie (takie rozwiązanie nazywa się często nieperturbacyjnym). W języku diagramów Feynmanna takie rozwiązanie opisywane jest przez tzw. diagram drabinowy (ang. ladder diagram), który wygląda następująco:

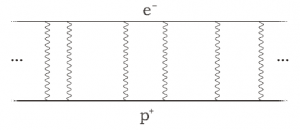
Otrzymuje się w ten sposób słynny wynik na energię stanu podstawowego elektronu -13.6 eV. Do otrzymanych rozwiązań równania Schroedingera dolicza się poprawki, obliczając diagramy Feynmanna z dorysowanaymi różnego rodzaju pętlami do diagramu drabinowego. Te obliczenia, jak też pomiary eksperymentalne poziomów energetycznych atomów, osiągnęły niezwykle wysoki poziom precyzji i są wspaniałym potwierdzeniem elektrodynamiki kwantowej.