Aby zrozumieć jak zmienia się przyspieszenie grawitacyjne wewnątrz Ziemi warto skorzystać z upraszczającego założenia oraz z trzech stwierdzeń.

Założenie które poczynimy jest takie, że Ziemia ma kształt kuli i jej gęstość jest wszędzie taka sama (tzn. materia w jej wnętrzu rozmieszczona jest jednorodnie).

Pierwsze stwierdzenie z którego skorzystamy jest takie, że kula o masie $M$ i stałej gęstości przyciąga przyciąga obiekty znajdujące się na zewnątrz niej w taki sam sposób, w jaki przyciągałby je punkt materialny o tej samej masie $M$.

Drugie stwierdzenie jest takie, że punkt materialny znajdujący się wewnątrz jednorodnie naładowanej kuli o promieniu $R$, w odległości $r$ od jej wnętrza (czyli $r<R$), jest przyciągany tylko przez część kuli zawartą wewnątrz promienia $r$. (To stwierdzenie wynika z faktu, że części kuli znajdujące się w odległości większej niż $r$ rozmieszczone są po obu stronach punktu umieszczonego w odległości $r$ i ich wkłady do przyspieszenia się znoszą.)

Trzeci istotny fakt to wzór na siłę oddziaływania grawitacyjnego między dwoma punktami o masach $M$ i $m$, oddalonymi od siebie o odległość $r$:

$$
F = G\frac{M\cdot m}{r^2},
$$

gdzie $G$ jest stałą grawitacji.

Zakładając, że ciało o masie $m$, znajdujące się na lub ponad powierzchnią Ziemi, w odległości $r$ od jej środka, porusza się z przyspieszeniem grawitacyjnym $g(r)$ w wyniku działania siły $F=mg$ którą możemy zidentyfikować z siłą daną powyższym wzorem, otrzymujemy wzór na przyspieszenie grawitacyjne

$$
g(r) = \frac{G\cdot M}{r^2},\qquad r\geq R
$$

gdzie teraz przez $R$ oznaczamy promień Ziemi. Zatem na zewnątrz Ziemi przyspieszenie maleje jak $1/r^2$.

Rozważmy teraz punkt o masie $m$ wewnątrz Ziemi, w odległości $r$ od jej środka. Zgodnie z drugim stwierdzeniem powyżej, działa na niego siła pochodząca tylko od kuli od promieniu $r$ (a nie od całej Ziemi której promień wynosi $R$). Zatem we wzorze na oddziaływanie grawitacyjne należy uwzględnić nie całkowitą masę Ziemi $M$, a jedynie masę jej części zawartą wewnątrz promienia $r$. Zakładając, że gęstość Ziemi jest stała, oraz biorąc pod uwagę, że objętość kuli $V=\frac{4}{3}\pi r^3$ proporcjonalna jest do trzeciej potęgi jej promienia, wnioskujemy, że masa zawarta wewnątrz promienia $r$ także skaluje się jak trzecia potęga promienia i wynosi zatem $M\frac{r^3}{R^3}$. W związku z tym wewnątrz Ziemi przyspieszenie wynosi

$$
g(r) = \frac{G\cdot M\frac{r^3}{R^3}}{r^2} = \frac{GM}{R^3}\cdot r,\qquad r<R
$$

czyli jest proporcjonalne do $r$.

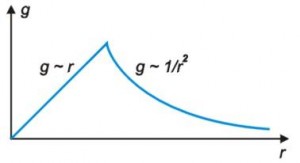
Pełna zależność przyspieszenia $g(r)$ od odległości od środka Ziemi przedstawiona jest na poniższym rysunku. W obszarze od $r=0$ do $r=R$ (gdzie $R$ to promień Ziemi) zależność ta jest liniowa, a dla $r>R$ maleje ona jak $1/r^2$.