Istnienie czarnych dziur jest jedną z bezpośrednich konsekwencji równań Einsteina. Mimo wieloletnich prac nad ich zrozumieniem, nadal sprawiają nam one pewne koncepcyjne problemy. Czarną dziurą możemy nazwać obszar czasoprzestrzeni, którego zakrzywienie jest tak duże, iż nawet światło nie jest go w stanie opuścić. Klasyczną czarną dziurą można też nazwać obszar do którego informacja może tylko „wlecieć” – informacja jest niszczona po przekroczeniu pewnej odległości od środka czarnej dziury zwanej horyzontem zdarzeń. Fakt, że czarna dziura jedynie pochłania informację a nic nie promieniuje, stoi w sprzeczności z teorią kwantową – Stephen Hawking w latach 70-tych udowodnił jednak, że czarne dziury promieniują.

Jak już wcześniej zaznaczono, istnienie czarnych dziur wynika z rozwiązań równań Einsteina, natomiast bezpośrednia obserwacja ich geometrii jest dosyć problematyczna, gdyż są ona właściwie nieobserwowalne przez nasze teleskopy. Dodatkowo, równania Einsteina są generalnie dosyć trudne do rozwiązywania i znalezienie ogólnych geometrycznych własności czarnych dziur może być niemal niewykonalne. Na szczęście istnieją pewne konkretne rozwiązania dla czarnych dziur, dla których potrafimy podać własności geometryczne.

Czarna dziura w metryce Schwarzschilda: metryka Schwarzschilda opisuje metrykę statycznej, sferycznej symetrycznej czarnej dziury (ogólniej opisuje metrykę wokół sferycznie symetrycznie rozłożonej masy). Dokładniej, rozwiązanie próżniowych równań Einsteina dla sferycznie symetrycznej masy przewiduje istnienie promienia zwanego promieniem Schwarzschilda. Każde ciało ściśnięte do rozmiarów kuli o promieniu mniejszym niż promień Schwarzschilda uformuje czarną dziurę. Jeśli obiekt zapadnie się do czarnej dziury to istotnie powierzchnia wyznaczająca horyzont zdarzeń ma kształt sferyczny. Przy czym w klasycznej teorii względności niewłaściwym jest myśleć, że znajduje się tam jakaś konkretna materia i można dotknąć „krawędzi” czarnej dziury; lepiej myśleć po prostu o obszarze, z którego nic nie wylatuje, tzn. stojąc obok czarnej dziury wizualnie nawet jej byśmy nie zauważyli (bo, przynajmniej nie uwzględniając zjawisk kwantowych, nie jest emitowane z niej promieniowanie). Wewnątrz czarnej dziury znajduje się osobliwość, czyli obszar o nieskończonej grawitacji, gdzie zgodnie z teorią klasyczną gęstość masy jest tak duża, że nie można już pominąć oddziaływań kwantowych i sama klasyczna teoria grawitacji nie wystarczy do opisu tego obszaru. Jak widać, geometria tej najprostszej czarnej dziury Schwarzschilda prowadzi do całkiem nietrywialnych przewidywań. Warto też zaznaczyć, że przestrzenne umiejscowienie osobliwości zawiera pewne subtelności. Zakładając, że cząstka wpada do czarnej dziury i jest przyciągana do osobliwości można zadać pytanie kiedy do niej doleci. Otóż czas własny, czyli czas zmierzony przez zegarek podróżujący razem z cząstką, jest nieskończony, czyli cząstka nigdy nie dotrze do samej osobliwości. Z tego powodu można też powiedzieć, że osobliwość znajduje się w przyszłości istnienia obiektów, które wpadły do czarnej dziury, a dokładnie na samym końcu ich istnienia.

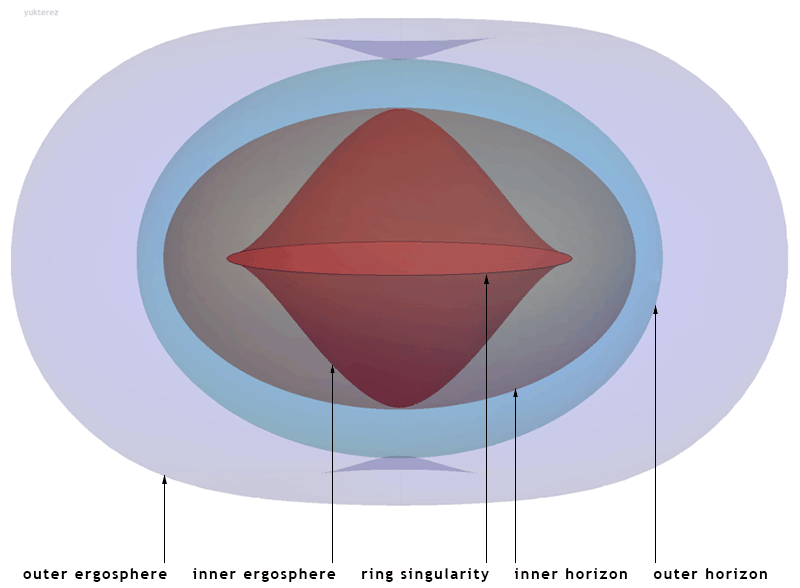
Z kolei czarna dziura w metryce Kerra to metryka nienaładowanej ładunkiem, rotującej czarnej dziury. Co ciekawe, metrykę Schwarschilda odkryto w roku 1915, czyli roku sformułowania przez Einsteina ogólnej teorii względności, natomiast rozwiązanie z obracającą się czarną dziurę znaleziono dopiero w roku 1963. Geometryczne własności metryki Kerra są dosyć skomplikowane, jednak można wyróżnić dwie charakterystyczne powierzchnie dla tej metryki. Pierwszą jest horyzont zdarzeń, który podobnie jak dla metryki Schwarzschilda jest obszarem czasoprzestrzeni, z którego informacja nie może się już wydostać. Drugim obszarem jest ergosfera, czyli obszar wokół czarnej dziury, taki że jeśli znajdzie się w nim pewien obiekt to zaczyna obracać się wraz z czarną dziurą. Jest to związane z efektem Lense-Thirringa, który zasadniczo stwierdza, że w obszarze ergosfery czarna dziura wprawia samą czasoprzestrzeń w ruch obrotowy i ciało obraca się wraz z czasoprzestrzenią. Aby cząstka dla odległego obserwatora wyglądała na stacjonarną to musiałaby się poruszać z prędkością większą niż światło (co jest niemożliwe), zatem dla obserwatora zewnętrznego cząstka się zawsze porusza w obszarze ergosfery. Warto zaznaczyć, że na to ciało nie działa żadna siła, ale jest to efekt nietrywialnej geometrii czasoprzestrzeni. Geometryczny obrazek metryki Kerra całkiem dobrze oddaje obrazek z Wikipedii.

Dodatkowe informacje o geometrii czasoprzestrzeni oraz ich prostych własności można znaleźć w wykładach wygłoszonych na Uniwersytecie Warszawskim profesorów Jerzego Lewandowskiego (wybitny specjalista w zakresie grawitacji kwantowej) oraz Andrzeja Dragana (specjalista w zakresie łączenia teorii względności z teorią kwantów).